


|
1.
Exploratory Data Analysis
1.3. EDA Techniques 1.3.6. Probability Distributions
|
|||
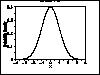
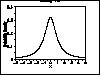
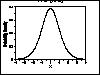
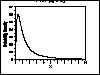
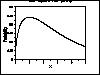
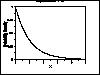
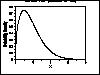
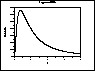
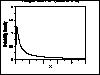
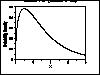
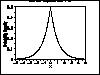
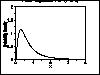
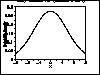
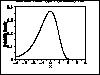
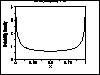
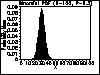
| Gallery of Common Distributions |
Detailed information on a few of the most common distributions
is available below. There are a large number of distributions
used in statistical applications. It is beyond the scope of this
Handbook to discuss more than a few of these. Two excellent sources
for additional detailed information on a large array of distributions
are Johnson, Kotz, and
Balakrishnan and
Evans, Hastings, and
Peacock.
Equations for the probability functions are given for the
standard form of the distribution.
Formulas exist for defining the
functions with location and scale parameters
in terms of the standard form of the distribution.
The sections on parameter estimation are restricted to the method of moments and maximum likelihood. This is because the least squares and PPCC and probability plot estimation procedures are generic. The maximum likelihood equations are not listed if they involve solving simultaneous equations. This is because these methods require sophisticated computer software to solve. Except where the maximum likelihood estimates are trivial, you should depend on a statistical software program to compute them. References are given for those who are interested. Be aware that different sources may give formulas that are different from those shown here. In some cases, these are simply mathematically equivalent formulations. In other cases, a different parameterization may be used. |
||
