1.3. EDA Techniques
1.3.3. Graphical Techniques: Alphabetic
1.3.3.16. |
Linear Correlation Plot |
Detect changes in correlation between groups
Linear correlation plots are often used in conjunction with linear slope, linear intercept, and linear residual standard deviation plots. A linear correlation plot could be generated intially to see if linear fitting would be a fruitful direction. If the correlations are high, this implies it is worthwhile to continue with the linear slope, intercept, and residual standard deviation plots. If the correlations are weak, a different model needs to be pursued.
In some cases, you might not have groups. Instead you may have different data sets and you want to know if the same correlation can be adequately applied to each of the data sets. In this case, simply think of each distinct data set as a group and apply the linear slope plot as for groups.
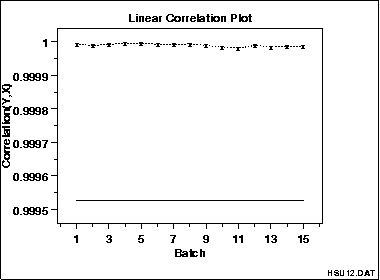
This linear correlation plot of the HSU12.DAT data set shows that the correlations are high for all groups. This implies that linear fits could provide a good model for each of these groups.
Group Correlations Versus Group ID
- Vertical axis: Group correlations
- Horizontal axis: Group identifier
- Are there linear relationships across groups?
- Are the strength of the linear relationships relatively constant across the groups?
Checking Group Homogeneity
Linear Slope Plot
Linear Residual Standard Deviation Plot
Linear Fitting

