1. Exploratory Data Analysis
1.3. EDA Techniques
1.3.3. Graphical Techniques: Alphabetic
1.3.3.10. Contour Plot

1.3.3.10.1.

DOE Contour Plot

DOE Contour Plot: Introduction

The DOE contour plot is a specialized contour plot used in the analysis of full and fractional experimental designs. These designs often have a low level, coded as "-1" or "-", and a high level, coded as "+1" or "+" for each factor. In addition, there can optionally be one or more center points. Center points are at the mid-point between the low and high level for each factor and are coded as "0".

The DOE contour plot is generated for two factors. Typically, this would be the two most important factors as determined by previous analyses (e.g., through the use of the DOE mean plots and an analysis of variance). If more than two factors are important, you may want to generate a series of DOE contour plots, each of which is drawn for two of these factors. You can also generate a matrix of all pairwise DOE contour plots for a number of important factors (similar to the scatter plot matrix for scatter plots).

The typical application of the DOE contour plot is in determining settings that will maximize (or minimize) the response variable. It can also be helpful in determining settings that result in the response variable hitting a pre-determined target value. The DOE contour plot plays a useful role in determining the settings for the next iteration of the experiment. That is, the initial experiment is typically a fractional factorial design with a fairly large number of factors. After the most important factors are determined, the DOE contour plot can be used to help define settings for a full factorial or response surface design based on a smaller number of factors.

Construction of DOE Contour Plot

The following are the primary steps in the construction of the DOE contour plot.

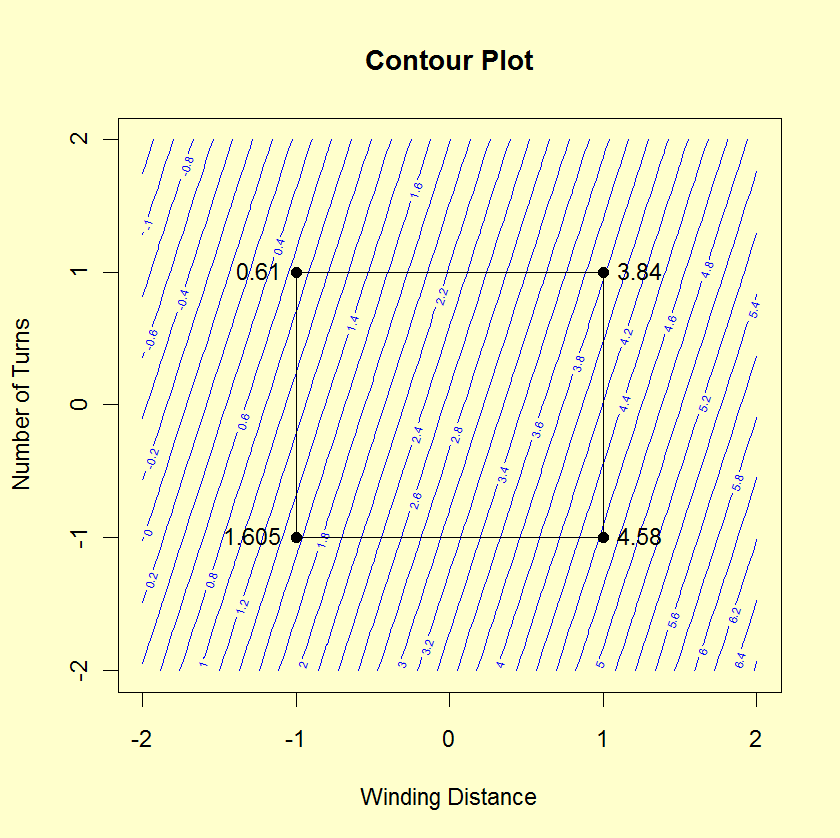
1. The x and y axes of the plot represent the values of the first and second factor (independent) variables.

2. The four vertex points are drawn. The vertex points are (-1,-1), (-1,1), (1,1), (1,-1). At each vertex point, the average of all the response values at that vertex point is printed.

3. Similarly, if there are center points, a point is drawn at (0,0) and the average of the response values at the center points is printed.

4. The linear DOE contour plot assumes the model:
   $$Y = \mu + \beta_1 \cdot U_1 + \beta_2 \cdot U_2 + \beta_{12} \cdot U_1 \cdot U_2 $$

   where μ is the overall mean of the response variable. The values of β₁, β₂, β₁₂, and μ are estimated from the vertex points using least squares estimation.

   In order to generate a single contour line, we need a value for Y, say Y₀. Next, we solve for U₂ in terms of U₁ and, after doing the algebra, we have the equation:

   $$\displaystyle{U_2 = \frac{(Y_0 - \mu) - \beta_1 \cdot U_1} {\beta_2 + \beta_{12} \cdot U_1}}$$

   We generate a sequence of points for U₁ in the range -2 to 2 and compute the corresponding values of U₂. These points constitute a single contour line corresponding to Y = Y₀.

   The user specifies the target values for which contour lines will be generated.

The above algorithm assumes a linear model for the design. DOE contour plots can also be generated for the case in which we assume a quadratic model for the design. The algebra for solving for U₂ in terms of U₁ becomes more complicated, but the fundamental idea is the same. Quadratic models are needed for the case when the average for the center points does not fall in the range defined by the vertex point (i.e., there is curvature).

Sample DOE Contour Plot

The following is a DOE contour plot for the data used in the Eddy current case study. The analysis in that case study demonstrated that X1 and X2 were the most important factors.

Interpretation of the Sample DOE Contour Plot

From the above DOE contour plot we can derive the following information.

1. Interaction significance;
2. Best (data) setting for these two dominant factors;

Interaction Significance

Note the appearance of the contour plot. If the contour curves are linear, then that implies that the interaction term is not significant; if the contour curves have considerable curvature, then that implies that the interaction term is large and important. In our case, the contour curves do not have considerable curvature, and so we conclude that the X1*X2 term is not significant.

Best Settings

To determine the best factor settings for the already-run experiment, we first must define what "best" means. For the Eddy current data set used to generate this DOE contour plot, "best" means to maximize (rather than minimize or hit a target) the response. Hence from the contour plot we determine the best settings for the two dominant factors by simply scanning the four vertices and choosing the vertex with the largest value (= average response). In this case, it is (X1 = +1, X2 = +1).

As for factor X3, the contour plot provides no best setting information, and so we would resort to other tools: the main effects plot, the interaction effects matrix, or the ordered data to determine optimal X3 settings.

Case Study

The Eddy current case study demonstrates the use of the DOE contour plot in the context of the analysis of a full factorial design.

Software

DOE Contour plots are available in many statistical software programs that analyze data from designed experiments.