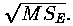
Main ANOVA Page SiRstv Dataset SiRstv Results
Certification Method and Definitions
Model:
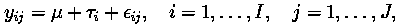
The general statistical model assumed for the 1-way balanced ANOVA problems is where I denotes the number of treatments and J denotes the number of replicates per treatment.
Methodology:
For all datasets, multiple precision calculations (accurate to 500 digits) were made using the preprocessor and FORTRAN subroutine package of Bailey (1995, available from NETLIB). Data were read in exactly as multiple precision numbers and all calculations were made with this very high precision. The results were output in multiple precision, and only then rounded to fifteen significant digits. These multiple precision results are an idealization. They represent what would be achieved if calculations were made without roundoff or other errors. Any typical numerical algorithm (i.e. not implemented in multiple precision) will introduce computational inaccuracies, and will produce results which differ slightly from these certified values.
Definitions:
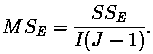
Within Treatment Sum of Squares The certified values for the within treatment sum of squares is defined by Within Treatment Degrees of Freedom The certified value of the within treatment degrees of freedom is defined by I(J - 1). Within Treatment Mean Square The certified value of the within treatment mean square is defined by Between Treatment Sum of Squares The certified values for the within treatment sum of squares is defined by Between Treatment Degrees of Freedom The certified value of the within treatment degrees of freedom is defined by (I - 1). 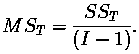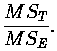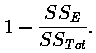Between Treatment Mean Square The certified value of the between treatment mean square is defined by F Statistics The certified value of the F statistics is defined by Total Sum of Squares The certified value of the total sum of squares is defined by R-Squared The certified value of the R-squared is defined by Residual Standard Deviation The certified value of the residual standard deviation is defined by