5. Process Improvement
5.5. Advanced topics

5.5.6.

What are Taguchi designs?

Taguchi designs are related to fractional factorial designs - many of which are large screening designs

Genichi Taguchi, a Japanese engineer, proposed several approaches to experimental designs that are sometimes called "Taguchi Methods." These methods utilize two-, three-, and mixed-level fractional factorial designs. Large screening designs seem to be particularly favored by Taguchi adherents.

Taguchi refers to experimental design as "off-line quality control" because it is a method of ensuring good performance in the design stage of products or processes. Some experimental designs, however, such as when used in evolutionary operation, can be used on-line while the process is running. He has also published a booklet of design nomograms ("Orthogonal Arrays and Linear Graphs," 1987, American Supplier Institute) which may be used as a design guide, similar to the table of fractional factorial designs given previously in Section 5.3. Some of the well-known Taguchi orthogonal arrays (L9, L18, L27 and L36) were given earlier when three-level, mixed-level and fractional factorial designs were discussed.

If these were the only aspects of "Taguchi Designs," there would be little additional reason to consider them over and above our previous discussion on factorials. "Taguchi" designs are similar to our familiar fractional factorial designs. However, Taguchi has introduced several noteworthy new ways of conceptualizing an experiment that are very valuable, especially in product development and industrial engineering, and we will look at two of his main ideas, namely Parameter Design and Tolerance Design.

Parameter Design

Taguchi advocated using inner and outer array designs to take into account noise factors (outer) and design factors (inner)

The aim here is to make a product or process less variable (more robust) in the face of variation over which we have little or no control. A simple fictitious example might be that of the starter motor of an automobile that has to perform reliably in the face of variation in ambient temperature and varying states of battery weakness. The engineer has control over, say, number of armature turns, gauge of armature wire, and ferric content of magnet alloy.

Conventionally, one can view this as an experiment in five factors. Taguchi has pointed out the usefulness of viewing it as a set-up of three inner array factors (turns, gauge, ferric %) over which we have design control, plus an outer array of factors over which we have control only in the laboratory (temperature, battery voltage).

Pictorial representation of Taguchi designs

Pictorially, we can view this design as being a conventional design in the inner array factors (compare Figure 3.1) with the addition of a "small" outer array factorial design at each corner of the "inner array" box.

Let I1 = "turns," I2 = "gauge," I3 = "ferric %," E1 = "temperature," and E2 = "voltage." Then we construct a 2³ design "box" for the I's, and at each of the eight corners so constructed, we place a 2² design "box" for the E's, as is shown in Figure 5.17.

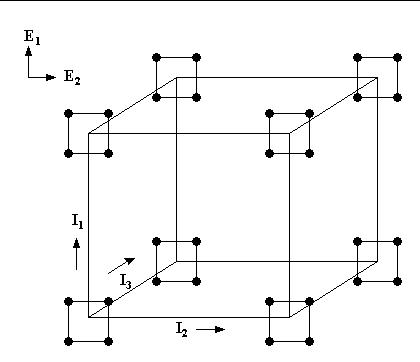
FIGURE 5.17: Inner 2³ and outer 2² arrays for robust design
with `I' the inner array, `E' the outer array.

An example of an inner and outer array designed experiment

We now have a total of 8x4 = 32 experimental settings, or runs. These are set out in Table 5.7, in which the 2³ design in the I's is given in standard order on the left of the table and the 2² design in the E's is written out sideways along the top. Note that the experiment would not be run in the standard order but should, as always, have its runs randomized. The output measured is the percent of (theoretical) maximum torque.

Table showing the Taguchi design and the responses from the experiment

TABLE 5.7: Design table, in standard order(s) for the parameter design of Figure 5.9

Run Number				1	2	3	4
	I1	I2	I3	E1 E2	-1 -1	+1 -1	-1 +1	+1 +1	Output MEAN	Output STD. DEV
1	-1	-1	-1		75	86	67	98	81.5	13.5
2	+1	-1	-1		87	78	56	91	78.0	15.6
3	-1	+1	-1		77	89	78	8	63.0	37.1
4	+1	+1	-1		95	65	77	95	83.0	14.7
5	-1	-1	+1		78	78	59	94	77.3	14.3
6	+1	-1	+1		56	79	67	94	74.0	16.3
7	-1	+1	+1		79	80	66	85	77.5	8.1
8	+1	+1	+1		71	80	73	95	79.8	10.9

(The reader can download the data as a text file.)

Interpretation of the table

Note that there are four outputs measured on each row. These correspond to the four `outer array' design points at each corner of the `outer array' box. As there are eight corners of the outer array box, there are eight rows in all.

Each row yields a mean and standard deviation % of maximum torque. Ideally there would be one row that had both the highest average torque and the lowest standard deviation (variability). Row 4 has the highest torque and row 7 has the lowest variability, so we are forced to compromise. We can't simply 'pick the winner.'

Use contour plots to see inside the box

One might also observe that all the outcomes occur at the corners of the design 'box', which means that we cannot see 'inside' the box. An optimum point might occur within the box, and we can search for such a point using contour plots. Contour plots were illustrated in the example of response surface design analysis given in Section 4.

Fractional factorials

Note that we could have used fractional factorials for either the inner or outer array designs, or for both.

Tolerance Design

Taguchi also advocated tolerance studies to determine, based on a loss or cost function, which variables have critical tolerances that need to be tightened

This section deals with the problem of how, and when, to specify tightened tolerances for a product or a process so that quality and performance/productivity are enhanced. Every product or process has a number, perhaps a large number, of components. We explain here how to identify the critical components to target when tolerances have to be tightened.

It is a natural impulse to believe that the quality and performance of any item can easily be improved by merely tightening up on some or all of its tolerance requirements. By this we mean that if the old version of the item specified, say, machining to ± 1 micron, we naturally believe that we can obtain better performance by specifying machining to ± ½ micron.

This can become expensive, however, and is often not a guarantee of much better performance. One has merely to witness the high initial and maintenance costs of such tight-tolerance-level items as space vehicles, expensive automobiles, etc. to realize that tolerance design, the selection of critical tolerances and the re-specification of those critical tolerances, is not a task to be undertaken without careful thought. In fact, it is recommended that only after extensive parameter design studies have been completed should tolerance design be performed as a last resort to improve quality and productivity.

Example

Example: measurement of electronic component made up of two components

Customers for an electronic component complained to their supplier that the measurement reported by the supplier on the as-delivered items appeared to be imprecise. The supplier undertook to investigate the matter.

The supplier's engineers reported that the measurement in question was made up of two components, which we label x and y, and the final measurement M was reported according to the standard formula

M = K x/y

with 'K' a known physical constant. Components x and y were measured separately in the laboratory using two different techniques, and the results combined by software to produce M. Buying new measurement devices for both components would be prohibitively expensive, and it was not even known by how much the x or y component tolerances should be improved to produce the desired improvement in the precision of M.

Taylor series expansion

Assume that in a measurement of a standard item the 'true' value of x is x_o and for y it is y_o. Let f(x, y) = M; then the Taylor Series expansion for f(x, y) is

\( \begin{array}{lcl} f(x,y) & = & f(x_{o},y_{o}) + (x - x_{o})\frac{df}{dx} + \\ & & (y - y_{o})\frac{df}{dy} + (x - x_{o})^{2}\frac{d^{2}f}{dx^{2}} \\ & & + (y - y_{o})^{2}\frac{d^{2}y}{dy^{2}} + (x - x_{o})(y - y_{o})\frac{d^{2}f}{dxdy} + \\ & & \mbox{(higher-order terms)} \end{array} \)

with all the partial derivatives, 'df/dx', etc., evaluated at (x_o, y_o).

Apply formula to M

Applying this formula to M(x, y) = Kx/y, we obtain

\( \begin{array}{lcl} M(x,y) & = & K\frac{x_o}{y_o} + (x - x_{o})\frac{K}{y_{o}} - (y - y_{o})\frac{Kx_{o}}{y_{o}^{2}} - \\ & & 2(y - y_{o})^{2}\frac{K}{y_{o}^{3}} - (x - x_{o})(y - y_{o})\frac{K}{y_{o}^{2}} \\ & & + \mbox{(higher-order terms)} \end{array} \)

It is assumed known from experience that the measurements of x show a distribution with an average value x_o, and with a standard deviation σ_x = 0.003 x-units.

Assume distribution of x is normal

In addition, we assume that the distribution of x is normal. Since 99.74% of a normal distribution's range is covered by 6σ, we take 3σ = 0.009 x-units to be the existing tolerance T_x for measurements on x. That is, T_x = ± 0.009 x-units is the 'play' around x_o that we expect from the existing measurement system.

Assume distribution of y is normal

It is also assumed known that the y measurements show a normal distribution around y_o, with standard deviation σ_y = 0.004 y-units. Thus T_y = ± 3σ_y = ±0.012.

Worst case values

Now ±T_x and ±T_y may be thought of as 'worst case' values for (x-x_o) and (y-y_o). Substituting T_x for (x-x_o) and T_y for (y-y_o) in the expanded formula for M(x, y), we have

\( \begin{array}{lcl} M_{T} & = & K\frac{x_o}{y_o} + T_{x}\frac{K}{y_{o}} - T_{y}\frac{Kx_{o}}{y_{o}^{2}} - 2 T_{y}^{2}\frac{K}{y_{o}^{3}} - T_{x}T_{y}\frac{K}{y_{o}^{2}} \\ & & + \mbox{(higher-order terms)} \end{array} \)

Drop some terms

The \( T_{y}^{2} \) and T_xT_y terms, and all terms of higher order, are going to be at least an order of magnitude smaller than terms in T_x and in T_y, and for this reason we drop them, so that \( M_{T} = K\frac{x_o}{y_o} + T_{x}\frac{K}{y_{o}} - T_{y}\frac{Kx_{o}}{y_{o}^{2}} \)

Worst case Euclidean distance

Thus, a 'worst case' Euclidean distance \( \delta \) of M(x, y) from its ideal value \( K \frac{x_{o}}{y_{o}} \) is (approximately)

\( \begin{array}{lcl} \Delta & = & \sqrt{\left( T_{x}\frac{K}{y_{o}} \right) ^2 + \left( T_{y}\frac{Kx_{o}}{y_{o}^{2}} \right) ^2} \\ & = & \sqrt{\left( 0.009 \frac{K}{y_{o}} \right) ^{2} + \left( 0.012 \frac{Kx_{o}}{y_{o}^{2}} \right) ^{2} } \end{array} \)

This shows the relative contributions of the components to the variation in the measurement.

Economic decision

As y_o is a known quantity and reduction in T_x and in T_y each carries its own price tag, it becomes an economic decision whether one should spend resources to reduce T_x or T_y, or both.

Simulation an alternative to Taylor series approximation

In this example, we have used a Taylor series approximation to obtain a simple expression that highlights the benefit of T_x and T_y. Alternatively, one might simulate values of M = K*x/y, given a specified (T_x,T_y) and (x₀,y₀), and then summarize the results with a model for the variability of M as a function of (T_x,T_y).

Functional form may not be available

In other applications, no functional form is available and one must use experimentation to empirically determine the optimal tolerance design. See Bisgaard and Steinberg (1997).