5. Process Improvement
5.3. Choosing an experimental design
5.3.3. How do you select an experimental design?
5.3.3.3. Full factorial designs

5.3.3.3.1.

Two-level full factorial designs

Description

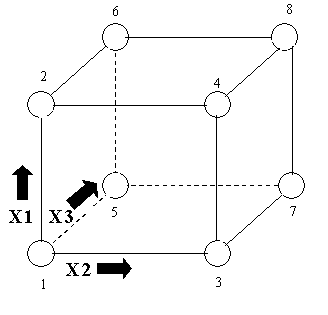
Graphical representation of a two-level design with 3 factors

Consider the two-level, full factorial design for three factors, namely the 2³ design. This implies eight runs (not counting replications or center point runs). Graphically, we can represent the 2³ design by the cube shown in Figure 3.1. The arrows show the direction of increase of the factors. The numbers `1' through `8' at the corners of the design box reference the `Standard Order' of runs (see Figure 3.1).

FIGURE 3.1  A 2³ two-level, full factorial design; factors X₁, X₂, X₃

The design matrix

In tabular form, this design is given by:

TABLE 3.3  A 2³ two-level, full factorial design table showing runs in `Standard Order'

run	X1	X2	X3
1	-1	-1	-1
2	1	-1	-1
3	-1	1	-1
4	1	1	-1
5	-1	-1	1
6	1	-1	1
7	-1	1	1
8	1	1	1

The left-most column of Table 3.3, numbers 1 through 8, specifies a (non-randomized) run order called the `Standard Order.' These numbers are also shown in Figure 3.1. For example, run 1 is made at the `low' setting of all three factors.

Standard Order for a 2^k Level Factorial Design

Rule for writing a 2^k full factorial in "standard order"

We can readily generalize the 2³ standard order matrix to a 2-level full factorial with k factors. The first (X₁) column starts with -1 and alternates in sign for all 2^k runs. The second (X₂) column starts with -1 repeated twice, then alternates with 2 in a row of the opposite sign until all 2^k places are filled. The third (X₃) column starts with -1 repeated 4 times, then 4 repeats of +1's and so on. In general, the i-th column (X_i) starts with 2^i-1 repeats of -1 folowed by 2^i-1 repeats of +1.

Example of a 2³ Experiment

Analysis matrix for the 3-factor complete factorial

An engineering experiment called for running three factors; namely, Pressure (factor X₁), Table speed (factor X₂) and Down force (factor X₃), each at a `high' and `low' setting, on a production tool to determine which had the greatest effect on product uniformity. Two replications were run at each setting. A (full factorial) 2³ design with 2 replications calls for 8*2=16 runs.

TABLE 3.4 Model or Analysis Matrix for a 2³ Experiment

Model Matrix								Response Variables
I	X1	X2	X1*X2	X3	X1*X3	X2*X3	X1*X2*X3	Rep 1	Rep 2
+1	-1	-1	+1	-1	+1	+1	-1	-3	-1
+1	+1	-1	-1	-1	-1	+1	+1	0	-1
+1	-1	+1	-1	-1	+1	-1	+1	-1	0
+1	+1	+1	+1	-1	-1	-1	-1	+2	+3
+1	-1	-1	+1	+1	-1	-1	+1	-1	0
+1	+1	-1	-1	+1	+1	-1	-1	+2	+1
+1	-1	+1	-1	+1	-1	+1	-1	+1	+1
+1	+1	+1	+1	+1	+1	+1	+1	+6	+5

The block with the 1's and -1's is called the Model Matrix or the Analysis Matrix. The table formed by the columns X₁, X₂ and X₃ is called the Design Table or Design Matrix.

Orthogonality Properties of Analysis Matrices for 2-Factor Experiments

Eliminate correlation between estimates of main effects and interactions

When all factors have been coded so that the high value is "1" and the low value is "-1", the design matrix for any full (or suitably chosen fractional) factorial experiment has columns that are all pairwise orthogonal and all the columns (except the "I" column) sum to 0.

The orthogonality property is important because it eliminates correlation between the estimates of the main effects and interactions.