7. Product and Process Comparisons
7.1. Introduction

7.1.6.

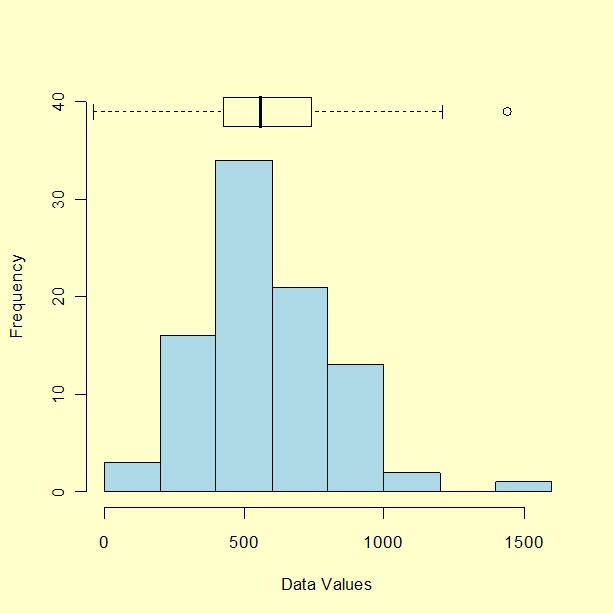
What are outliers in the data?

Definition of outliers

An outlier is an observation that lies an abnormal distance from other values in a random sample from a population. In a sense, this definition leaves it up to the analyst (or a consensus process) to decide what will be considered abnormal. Before abnormal observations can be singled out, it is necessary to characterize normal observations.

Ways to describe data

Two activities are essential for characterizing a set of data:

1. Examination of the overall shape of the graphed data for important features, including symmetry and departures from assumptions. The chapter on Exploratory Data Analysis (EDA) discusses assumptions and summarization of data in detail.

2. Examination of the data for unusual observations that are far removed from the mass of data. These points are often referred to as outliers. Two graphical techniques for identifying outliers, scatter plots and box plots, along with an analytic procedure for detecting outliers when the distribution is normal (Grubbs' Test), are also discussed in detail in the EDA chapter.

Box plot construction

The box plot is a useful graphical display for describing the behavior of the data in the middle as well as at the ends of the distributions. The box plot uses the median and the lower and upper quartiles (defined as the 25th and 75th percentiles). If the lower quartile is Q1 and the upper quartile is Q3, then the difference (Q3 - Q1) is called the interquartile range or IQ.

Box plots with fences

A box plot is constructed by drawing a box between the upper and lower quartiles with a solid line drawn across the box to locate the median. The following quantities (called fences) are needed for identifying extreme values in the tails of the distribution:

1. lower inner fence: Q1 - 1.5*IQ
2. upper inner fence: Q3 + 1.5*IQ
3. lower outer fence: Q1 - 3*IQ
4. upper outer fence: Q3 + 3*IQ

Outlier detection criteria

A point beyond an inner fence on either side is considered a mild outlier. A point beyond an outer fence is considered an extreme outlier.

Example of an outlier box plot

The data set of N = 90 ordered observations as shown below is examined for outliers:

30, 171, 184, 201, 212, 250, 265, 270, 272, 289, 305, 306, 322, 322, 336, 346, 351, 370, 390, 404, 409, 411, 436, 437, 439, 441, 444, 448, 451, 453, 470, 480, 482, 487, 494, 495, 499, 503, 514, 521, 522, 527, 548, 550, 559, 560, 570, 572, 574, 578, 585, 592, 592, 607, 616, 618, 621, 629, 637, 638, 640, 656, 668, 707, 709, 719, 737, 739, 752, 758, 766, 792, 792, 794, 802, 818, 830, 832, 843, 858, 860, 869, 918, 925, 953, 991, 1000, 1005, 1068, 1441

The above data is available as a text file.

The computations are as follows:

• Median = (n+1)/2 largest data point = the average of the 45th and 46th ordered points = (559 + 560)/2 = 559.5
• Lower quartile = .25(N+1)th ordered point = 22.75th ordered point = 411 + .75(436-411) = 429.75
• Upper quartile = .75(N+1)th ordered point = 68.25th ordered point = 739 +.25(752-739) = 742.25
• Interquartile range = 742.25 - 429.75 = 312.5
• Lower inner fence = 429.75 - 1.5 (312.5) = -39.0
• Upper inner fence = 742.25 + 1.5 (312.5) = 1211.0
• Lower outer fence = 429.75 - 3.0 (312.5) = -507.75
• Upper outer fence = 742.25 + 3.0 (312.5) = 1679.75

From an examination of the fence points and the data, one point (1441) exceeds the upper inner fence and stands out as a mild outlier; there are no extreme outliers.

Histogram with box plot

A histogram with an overlaid box plot are shown below. The outlier is identified as the largest value in the data set, 1441, and appears as the circle to the right of the box plot.

Outliers may contain important information

Outliers should be investigated carefully. Often they contain valuable information about the process under investigation or the data gathering and recording process. Before considering the possible elimination of these points from the data, one should try to understand why they appeared and whether it is likely similar values will continue to appear. Of course, outliers are often bad data points.