1.3. EDA Techniques
1.3.5. Quantitative Techniques
1.3.5.3. |
Two-Sample t-Test for Equal Means |
Test if two population means are equal
There are several variations on this test.
- The data may either be paired or not paired. By paired, we mean that there is a one-to-one correspondence between the values in the two samples. That is, if X1, X2, ..., Xn and Y1, Y2, ... , Yn are the two samples, then Xi corresponds to Yi. For paired samples, the difference Xi - Yi is usually calculated. For unpaired samples, the sample sizes for the two samples may or may not be equal. The formulas for paired data are somewhat simpler than the formulas for unpaired data.
- The variances of the two samples may be assumed to be equal or unequal. Equal variances yields somewhat simpler formulas, although with computers this is no longer a significant issue.
- In some applications, you may want to adopt a new process or treatment only if it exceeds the current treatment by some threshold. In this case, we can state the null hypothesis in the form that the difference between the two populations means is equal to some constant \(\mu_{1} - \mu_{2} = d_{0}\) where the constant is the desired threshold.
| H0: | \( \mu_{1} = \mu_{2} \) |
| Ha: | \( \mu_{1} \neq \mu_{2} \) |
| Test Statistic: |
\( T = \frac{\bar{Y_{1}} - \bar{Y_{2}}}
{\sqrt{{s^{2}_{1}}/N_{1} + {s^{2}_{2}}/N_{2}}} \)
where N1 and N2 are the sample sizes, \( \bar{Y_{1}} \) and \( \bar{Y_{2}} \) are the sample means, and \( {s^{2}_{1}} \) and \( {s^{2}_{2}} \) are the sample variances. If equal variances are assumed, then the formula reduces to:
|
|
Significance Level:
|
α. |
| Critical Region: |
Reject the null hypothesis that the two means are equal if
|
SAMPLE 1:
NUMBER OF OBSERVATIONS = 249
MEAN = 20.14458
STANDARD DEVIATION = 6.41470
STANDARD ERROR OF THE MEAN = 0.40652
SAMPLE 2:
NUMBER OF OBSERVATIONS = 79
MEAN = 30.48101
STANDARD DEVIATION = 6.10771
STANDARD ERROR OF THE MEAN = 0.68717
We are testing the hypothesis that the population means are equal for the two samples. We assume that the variances for the two samples are equal.
H0: μ1 = μ2 Ha: μ1 ≠ μ2The absolute value of the test statistic for our example, 12.62059, is greater than the critical value of 1.9673, so we reject the null hypothesis and conclude that the two population means are different at the 0.05 significance level.Test statistic: T = -12.62059 Pooled standard deviation: sp = 6.34260 Degrees of freedom: ν = 326 Significance level: α = 0.05 Critical value (upper tail): t1-α/2,ν = 1.9673 Critical region: Reject H0 if |T| > 1.9673
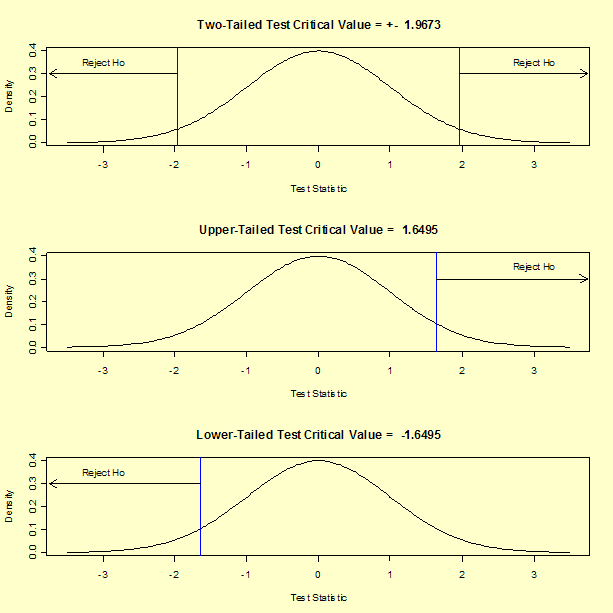
In general, there are three possible alternative hypotheses and rejection regions for the one-sample t-test:
| Alternative Hypothesis | Rejection Region |
|---|---|
| Ha: μ1 ≠ μ2 | |T| > t1-α/2,ν |
| Ha: μ1 > μ2 | T > t1-α,ν |
| Ha: μ1 < μ2 | T < tα,ν |
For our two-tailed t-test, the critical value is t1-α/2,ν = 1.9673, where α = 0.05 and ν = 326. If we were to perform an upper, one-tailed test, the critical value would be t1-α,ν = 1.6495. The rejection regions for three posssible alternative hypotheses using our example data are shown below.
- Is process 1 equivalent to process 2?
- Is the new process better than the current process?
- Is the new process better than the current process by at least some pre-determined threshold amount?
Analysis of Variance

