WAKCDF

WAKCDF (LET)

Library Function

Compute the Wakeby cumulative distribution function.

The Wakeby distribution is defined by the transformation

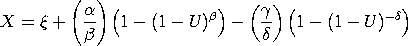
where U is a standard uniform random variable. That is, the above equation defines the percent point function for the Wakeby distribution.

The parameters , and are shape parameters. The parameter is a location parameter and the parameter is a scale parameter.

The following restrictions apply to the parameters of this distribution:

1. + ≥ 0
2. Either + > 0 or = = = 0
3. If > 0, then > 0
4. ≥ 0
5. + ≥ 0

The domain of the Wakeby distribution is

1. to
   if ≥ 0 and > 0
2. to + (/ ) - (/ )
   if < 0 or = 0

With three shape parameters, the Wakeby distribution can model a wide variety of shapes.

The cumulative distribution function is computed by numerically inverting the percent point function given above.

LET <y> = WAKCDF(<x>,<beta>,<gamma>,<delta>,<chi>,<alpha>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a number, parameter, or variable;
            <y> is a variable or a parameter (depending on what <x> is) where the computed Wakeby cdf value is stored;
            <beta> is a number, parameter, or variable that specifies the first shape parameter;
            <gamma> is a number, parameter, or variable that specifies the second shape parameter;
            <delta> is a number, parameter, or variable that specifies the third shape parameter;
            <chi> is a number, parameter, or variable that specifies the location parameter;
            <alpha> is a number, parameter, or variable that specifies the scale parameter;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

If <xi> and <alpha> are omitted, they default to 0 and 1, respectively.

LET A = WAKCDF(1.3,2.5,6)
LET A = WAKCDF(13,2.5,6,0,10)
PLOT WAKCDF(X,2.5,6) FOR X = -10 0.1 10

The cumulative distribution function for the Wakeby distribution is computed using the CDFWAK routine written by Hosking (see the Reference section below).

Hoskings report and associated Fortran code can be downloaded from the Statlib archive at

http://lib.stat.cmu.edu/

None

None

WAKPDF	Compute the Wakeby probability density function.
WAKPPF	= Compute the Wakeby percent point function.
GEPPDF	= Compute the generalized Pareto probability density function.
GEVPDF	= Compute the generalized extreme value probability density function.
WEIPDF	= Compute the Weibull probability density function.
LGNPDF	= Compute the lognormal probability density function.
LAMPDF	Compute the Tukey lambda probability density function.
GLDPDF	= Compute the generalized Tukey lambda probability density function.
GHPDF	= Compute the g and h probability density function.

Johnson, Kotz, and Balakrishnan (1994), "Continuous Univariate Distribution--Volume 1", Second Edition, Wiley, pp. 44-47.

J. R. M. Hosking (2000), "Research Report: Fortran Routines for use with the Method of L-Moments", IBM Research Division, T. J. Watson Research Center, Yorktown Heights, NY 10598.

Hoskings (1990), "L-moments: Analysis and Estimation of Distribution using Linear Combinations of Order Statistics", Journal of the Royal Statistical Society, Series B, 52, pp. 105-124.

Distributional Modeling

2007/10

 
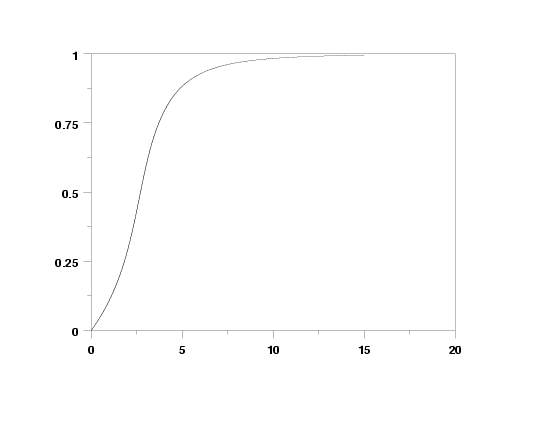
let xi = 0
let alpha = 10
let beta = 5
let gamma = 1
let delta = 0.3
.
plot wakcdf(x,beta,gamma,delta,xi,alpha) for x = .01 .01 15