TRIMMED STANDARD DEVIATION

TRIMMED STANDARD DEVIATION (LET)

Let Subcommand

Compute the trimmed standard deviation for a variable.

The standard deviation of a variable is defined as

with n and 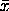denoting the sample size and the sample mean, respectively. The standard deviation can be heavily influenced by extreme values (i.e., it is not robust). The trimmed standard deviation compensates for this by dropping a certain percentage of values from the tails. For example, the 50% trimmed standard deviation is the standard deviation of the values between the upper and lower quartiles. The 90% trimmed standard deviation is the standard deviation of the values after truncating the lowest and highest 5% of the values.

LET <a> = TRIMMED STANDARD DEVIATION <y>
                        <SUBSET/EXCEPT/FOR qualification>
where <y> is the response variable;
            <a> is a parameter where the computed trimmed sd is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = TRIMMED STANDARD DEVIATION Y1
LET A = TRIMMED STANDARD DEVIATION Y1 SUBSET TAG > 2

The analyst must specify the percentages to trim in each tail. This is done by defining the internal variables P1 (the lower tail) and P2 (the upper tail). For example, to trim 10% off each tail, do the following:
LET P1 = 10
LET P2 = 10
LET A = TRIMMED STANDARD DEVIATION Y

Support for the trimmed standard deviation has been added to the following plots and commands:
LET P1 = 10
LET P2 = 10


TRIMMED STANDARD DEVIATION PLOT Y X
CROSS TABULATE TRIMMED STANDARD DEVIATION PLOT Y X1 X2
BOOTSTRAP TRIMMED STANDARD DEVIATION PLOT Y
JACKNIFE TRIMMED STANDARD DEVIATION PLOT Y
DEX TRIMMED STANDARD DEVIATION PLOT Y X1 ... XK
TRIMMED STANDARD DEVIATION BLOCK PLOT Y X1 .... XK
TRIMMED STANDARD DEVIATION INFLUENCE CURVE Y


TABULATE TRIMMED STANDARD DEVIATION Y X1
CROSS TABULATE TRIMMED STANDARD DEVIATION Y X1 X2
LET Y2 = CROSS TABULATE TRIMMED STANDARD DEVIATION ...
            Y X1 X2
LET V = MATRIX TRIMMED STANDARD DEVIATION M

None

TRIMMED SD

STATISTIC PLOT	= Generate a statistic vs. subset plot.
STANDARD DEVIATION	= Compute the standard deviation.
WINSORIZED SD	= Compute the Winsorized sd.
BIWEIGHT SCALE	= Compute the biweight scale statistic.
TRIMMED MEAN	= Compute the trimmed mean.

Robust Data Analysis

2007/5

 
    LET Y1 = CAUCHY RANDOM NUMBERS FOR I = 1 1 100
    LET P1 = 10
    LET P2 = 10
    LET A1 = TRIMMED STANDARD DEVIATION Y1