SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

SEMPPF

Name:
    SEMPPF (LET)
Type:
    Library Function
Purpose:
    Compute the semi-circular percent point function.
Description:
    The semi-circular distribution is the distribution onto one axis of the points uniformly distributed within the unit circle. As such, it is useful for testing 2-dimensional uniformity.

    The formula for the cumulative distribution function is:

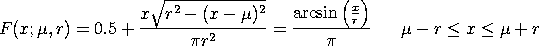
      F(x;mu,r) = 0.5 + x*SQRT(r**2 - (x-mu)**2)/(PI*r**2) + ARCSIN((x-mu)/r)/PI -r <= x <= r

    with mu and r denoting the location and scale parameters, respectively.

    The percent point function is computed by numerically inverting the cumulative distribution function.

    The case where mu = 0 and r = 1 is referred to as the standard semi-circular distribution.

Syntax:
    LET <y> = SEMPPF(<p>,<mu>,<r>)
                            <SUBSET/EXCEPT/FOR qualification>
    where <p> is a variable, number, or parameter in the interval (0,1);
                <mu> is a variable, number, or parameter that specifies the location parameter;
                <r> is a variable, number, or parameter that specifies the scale parameter;
                <y> is a variable or a parameter (depending on what <p> is) where the computed semi-circular ppf value is stored;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.

    If <mu> and <r> are omitted, they default to 0 and 1, respectively.

Examples:
    LET A = SEMPPF(0.99)
    LET A = SEMPPF(0.99,0,5)
    LET X2 = SEMPPF(X1)
Default:
    None
Synonyms:
    None
Related Commands:
    SEMCDF = Compute the semi-circular cumulative distribution function.
    SEMPDF = Compute the semi-circular probability density function.
    UNIPDF = Compute the uniform probability density function.
    UNICDF = Compute the uniform cumulative distribution function.
    UNIPPF = Compute the uniform percent point function.
    NORCDF = Compute the normal cumulative distributoin function.
    NORPDF = Compute the normal probability density function.
    NORPPF = Compute the normal percent point function.
Reference:
    Johnson and Kotz (1970), Continuous Univariate Distributions - 2, Houghton Mifflin, (chapter 25).

    Filliben (1969), Simple and Robust Linear Estimation of the Location Parameter of a Symmetric Distribution, unpublished Ph.d dissertation, Princeton University, (pp. 21-44, 229-231).

Applications:
    Distributional Modeling
Implementation Date:
    1994/4: Implemented for the standard case
    2006/10: Implemented for the general case
Program: 
     
XLIMITS 0 1
MAJOR XTIC NUMBER 6
MINOR XTIC NUMBER 1
XTIC DECIMAL 1
YLIMITS -1 1
YTIC OFFSET 0.1 0.1
TITLE AUTOMATIC
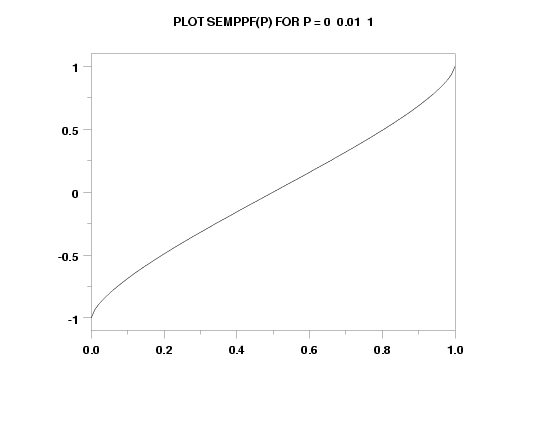
PLOT SEMPPF(X) FOR X = 0.01 .01 0.99
    plot generated by sample program

Date created: 1/8/2008
Last updated: 1/8/2008
Please email comments on this WWW page to [email protected].