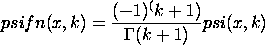PSIFN

PSIFN (LET)

Library Function

Compute the scaled kth derivative of the digamma (or psi) function.

The psifn function is defined as:

where 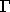is the gamma function and PSI(X,K) is the kth derivative of the digamma function. Enter HELP DIGAMMA for details on the digamma function.

Note that this is the kth derivative of the digamma function, not the log gamma function. That is, for k=1, the trigamma function is computed, not the digamma function.

LET <y> = PSIFN(<x>)             <SUBSET/EXCEPT/FOR qualification>
where <x> is a number, variable or a parameter;
              <y> is a variable or a parameter (depending on what <x> is) where the computed psifn values are stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = PSIFN(1,2)
LET X2 = PSIFN(X1,K)

DATAPLOT uses the routine PSIFN from the SLATEC Common Mathematical Library to compute this function. SLATEC is a large set of high quality, portable, public domain Fortran routines for various mathematical capabilities maintained by seven federal laboratories.

None

None

GAMMA	= Compute the gamma function.
DIGAMMA	= Compute the digamma function.
LOGGAMMA	= Compute the log (to base e) gamma function.
GAMMAI	= Compute the incomplete Gamma function.
GAMMAIP	= Compute an alternate form of the incomplete gamma function.
GAMMAIC	= Compute the complementary incomplete Gamma function.
GAMMAR	= Compute the reciprocal gamma function.
TRICOMI	= Compute Tricomi's incomplete gamma function.
BETA	= Compute the Beta function.

"Handbook of Mathematical Functions, Applied Mathematics Series, Vol. 55", Abramowitz and Stegun, National Bureau of Standards, 1964 (chapter 6).

Special Functions

1998/5

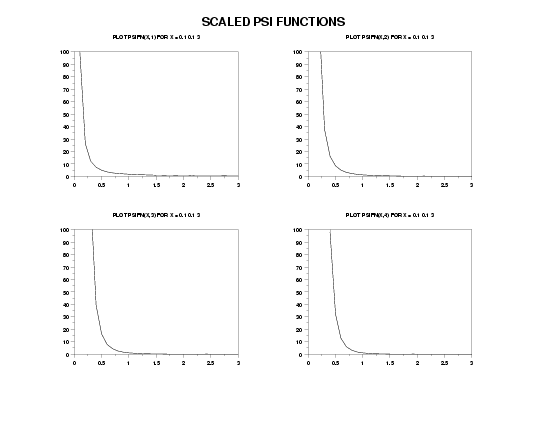
YLIMITS 0 100
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 5 5 95 95
TITLE AUTOMATIC
PLOT PSIFN(X,1) FOR X = 0.1 0.1 3
PLOT PSIFN(X,2) FOR X = 0.1 0.1 3
PLOT PSIFN(X,3) FOR X = 0.1 0.1 3
PLOT PSIFN(X,4) FOR X = 0.1 0.1 3
END OF MULTIPLOT
MOVE 50 97
JUSTIFICATION CENTER
TEXT SCALED PSI FUNCTIONS