

|
NCFPDFName:
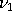 and and
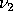 and with
non-centrality parameter and with
non-centrality parameter
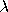 . .
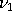 and and
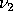 ,
respectively, then ,
respectively, then
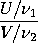
follows a F distribution. If U is replaced with a
non-central chi-square distribution with non-centrality
parameter
The probability density function of the non-central F
distribution is rather complicated and not given here. It is
given on page 95 of Evans, Hastings, and Peacock (see the
Reference section below). The input value and both degrees of
freedom parameters should be positive and the non-centrality
parameter should be non-negative
( The non-central F distribution can be generalized with location and scale parameters in the usual way.
<SUBSET/EXCEPT/FOR qualification> where <x> is a number, variable or a parameter containing non-negative values; <v1> is a non-negative number, parameter or variable that specifies the first degrees of freedom parameter; <v2> is a non-negative number, parameter or variable that specifies the second degrees of freedom parameter; <lambda> is a non-negative number, parameter or variable that specifies the non-centrality parameter; <loc> is a number or parameter that specifies the location parameter; <scale> is a number or parameter that specifies the scale parameter; <y> is a variable or a parameter (depending on what <y1> is) where the computed pdf value is stored; and where the <SUBSET/EXCEPT/FOR qualification> is optional. Note that the location and scale parameters are optional.
LET A = NCFPDF(2,10,10,5) LET X2 = NCFPDF(1.1,14,15,10000)
DATAPLOT computes the non-central F distribution by converting it to an equivalent non-central beta distribution. It then uses algorithm AS 226 (see the REFERENCE section below) obtained from the statlib archive to compute the non-central beta cdf. It uses the DBETAI and DLNGAM routines from the SLATEC library rather than the corresponding algorithms from the Applied Statistics series to compute the log gamma and incomplete beta functions.
LET NU2 = <value> LET LAMBDA = <value> LET Y = NON-CENTRAL F RANDOM NUMBERS FOR I = 1 1 N To generate a non-central F probability plot or an non-central F Kolmogorov-Smirnov or chi-square goodness of fit test, enter the following commands
LET NU2 = <value> LET LAMBDA = <value> NON-CENTRAL F PROBABILITY PLOT Y NON-CENTRAL F KOLMOGOROV SMIRNOV GOODNESS OF FIT Y NON-CENTRAL F CHI-SQUARE GOODNESS OF FIT Y
"Continuous Univariate Distributions: Volume 2", Johnson, Kotz, and Balakrishnan, Wiley and Sons, 1994, chapter 30. "Statistical Distributions", Third Edition, Evans, Hastings, and Peacock, 2000 pp. 95-97.
LABEL CASE ASIS
Y1LABEL Probability
X1LABEL X
Y1LABEL DISPLACEMENT 12
X1LABEL DISPLACEMENT 12
TITLE DISPLACEMENT 2
Y1LIMITS 0 0.7
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
MULTIPLOT 2 2
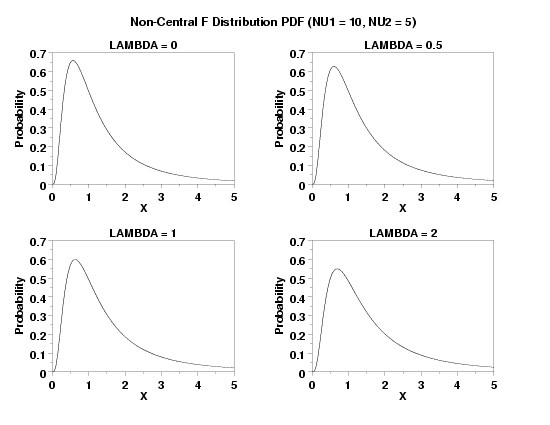
TITLE LAMBDA = 0
PLOT NCFPDF(X,10,5,0) FOR X = 0.01 0.01 5
TITLE LAMBDA = 0.5
PLOT NCFPDF(X,10,5,0.5) FOR X = 0.01 0.01 5
TITLE LAMBDA = 1
PLOT NCFPDF(X,10,5,1) FOR X = 0.01 0.01 5
TITLE LAMBDA = 2
PLOT NCFPDF(X,10,5,2) FOR X = 0.01 0.01 5
END OF MULTIPLOT
CASE ASIS
JUSTIFICATION CENTER
MOVE 50 97
TEXT Non-Central F Distribution PDF (NU1 = 10, NU2 = 5)
Date created: 7/7/2004 |