MUTPDF

MUTPDF (LET)

Library Function

Compute the Muth probability density function with shape parameter .

The standard Muth distribution has the following probability density function:

with denoting the shape parameter.

This distribution can be generalized with location and scale parameters in the usual way using the relation

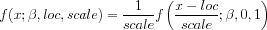
with <loc> and <scale> denoting the location and scale parameters, respectively.

LET <y> = MUTPDF(<x>,<beta>,<loc>,<scale>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a number, parameter, or variable;
            <y> is a variable or a parameter (depending on what <x> is) where the computed Muth pdf value is stored;
            <beta> is a number, parameter, or variable that specifies the shape parameter;
            <loc> is a number, parameter, or variable that specifies the location parameter;
            <scale> is a positive number, parameter, or variable that specifies the scale parameter;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

If <loc> and <scale> are omitted, they default to 0 and 1, respectively.

LET A = MUTPDF(0.3,0.2)
LET Y = MUTPDF(X,0.5,0,5)
PLOT MUTPDF(X,0.7,0,3) FOR X = 0 0.01 5

Muth random numbers, probability plots, and goodness of fit tests can be generated with the commands:
LET BETA = <value>
LET Y = MUTH RANDOM NUMBERS FOR I = 1 1 N
MUTH PROBABILITY PLOT Y
MUTH PROBABILITY PLOT Y2 X2
MUTH PROBABILITY PLOT Y3 XLOW XHIGH
MUTH KOLMOGOROV SMIRNOV GOODNESS OF FIT Y
MUTH CHI-SQUARE GOODNESS OF FIT Y2 X2
MUTH CHI-SQUARE GOODNESS OF FIT Y3 XLOW XHIGH


The following commands can be used to estimate the shape parameter for the Muth distribution:

LET BETA1 = <value>
LET BETA2 = <value>
MUTH PPCC PLOT Y
MUTH PPCC PLOT Y2 X2
MUTH PPCC PLOT Y3 XLOW XHIGH
MUTH KS PLOT Y
MUTH KS PLOT Y2 X2
MUTH KS PLOT Y3 XLOW XHIGH


The default values for BETA1 and BETA2 are 0 and 1.

The probability plot can then be used to estimate the location and scale (location = PPA0, scale = PPA1).

The BOOTSTRAP DISTRIBUTION command can be used to find uncertainty intervals for the ppcc and ks plots.

None

None

MUTCDF	= Compute the Muth cumulative distribution function.
MUTCHAZ	= Compute the Muth cumulative hazard function.
MUTHAZ	= Compute the Muth hazard function.
MUTPPF	= Compute the Muth percent point function.
RAYPDF	= Compute the Rayleigh probability density function.
WEIPDF	= Compute the Weibull probability density function.
LGNPDF	Compute the lognormal probability density function.
EXPPDF	= Compute the exponential probability density function.
LOGPDF	= Compute the logistic probability density function.
GAMPDF	= Compute the gamma probability density function.
EWEPDF	= Compute the exponentiated Weibull probability density function.
B10PDF	= Compute the Burr type 10 probability density function.

Leemis and McQuestion (2008), "Univariate Distribution Relationships", The American Statistician, Vol. 62, No. 1, pp. 45-53.

Muth (1977), "Reliability Models with Positive Memory Derived from the Mean Residual Life Function", in The Theory and Applications of Reliability, Eds. Tsokos and Shimi, New York: Academic Press Inc., pp. 401-435.

Distributional Modeling

2008/2

 
LABEL CASE ASIS
TITLE CASE ASIS
TITLE OFFSET 2
.
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
.
LET BETA  = 0.2
TITLE BETA = ^BETA
PLOT MUTPDF(X,BETA) FOR X = 0.01  0.01  5
.
LET BETA  = 0.5
TITLE BETA = ^BETA
PLOT MUTPDF(X,BETA) FOR X = 0.01  0.01  5
.
LET BETA  = 0.7
TITLE BETA = ^BETA
PLOT MUTPDF(X,BETA) FOR X = 0.01  0.01  5
.
LET BETA  = 1
TITLE BETA = ^BETA
PLOT MUTPDF(X,BETA) FOR X = 0.01  0.01  5
.
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 97
TEXT Muth Probability Density Functions
 
    

    
       
    
    

    

 
let beta = 0.65
let betasav = beta
.
let y = muth random numbers for i = 1 1 200
let y = 10*y
let amax = maximum y
.
label case asis
title case asis
.
y1label Correlation Coefficient
x1label Beta
muth ppcc plot y
let beta = shape
justification center
move 50 6
text Betahat = ^beta (BETA = ^betasav)
move 50 2
text Maximum PPCC = ^maxppcc
.
y1label Data
x1label Theoretical
char x
line bl
muth prob plot y
move 50 6
text Location = ^ppa0, Scale = ^ppa1
char bl
line so
.
y1label Relative Frequency
x1label
relative hist y
limits freeze
pre-erase off
line color blue
plot mutpdf(x,beta,ppa0,ppa1) for x = 0.01 .01 amax
line color black
limits 
pre-erase on
.
let ksloc = ppa0
let ksscale = ppa1
muth kolmogorov smirnov goodness of fit y
    


    
       
    
    


    
       
    
    


    
       
    
    


    
    
                   KOLMOGOROV-SMIRNOV GOODNESS-OF-FIT TEST
  
 NULL HYPOTHESIS H0:      DISTRIBUTION FITS THE DATA
 ALTERNATE HYPOTHESIS HA: DISTRIBUTION DOES NOT FIT THE DATA
 DISTRIBUTION:            MUTH
    NUMBER OF OBSERVATIONS              =      200
  
 TEST:
 KOLMOGOROV-SMIRNOV TEST STATISTIC      =   0.3268123E-01
  
    ALPHA LEVEL         CUTOFF              CONCLUSION
            10%       0.086*              ACCEPT H0
                      0.085**
             5%       0.096*              ACCEPT H0
                      0.095**
             1%       0.115*              ACCEPT H0
                      0.114**
  
     *  - STANDARD LARGE SAMPLE APPROXIMATION  ( C/SQRT(N) )
    ** - MORE ACCURATE LARGE SAMPLE APPROXIMATION  ( C/SQRT(N + SQRT(N/10)) )