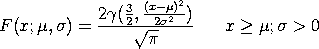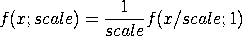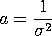SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

MAXCDF

Name:
    MAXCDF (LET)
Type:
    Library Function
Purpose:
    Compute the Maxwell-Boltzman cumulative distribution function.
Description:
    The Maxwell-Boltzman distribution has the following cumulative distribution function:

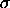      F(x;sigma)=2*GAMMAI(3/2,0.5*(1/sigma**2)*x**2)/SQRT(PI) x >= 0; sigma > 0

    with sigma denoting the scale parameter and 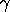GAMMAI denoting the incomplete gamma function.

    If 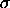sigma = 1, the Maxwell-Boltzman distribution is equivalent to the standard chi distribution with 3 degrees of freedom.

    Note that 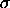sigma is essentially a scale parameter. However, it is not strictly a scale parameter in the sense that the following relationship does not hold:

      f(x;scale) = (1/scale)*f(x/scale;1)

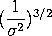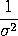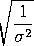    The (1/sigma^2)^(3/2) term would have to be 1/sigma^2 for this relationship to hold (that is, there is an extra SQRT(1/sigma^2) term).

    The Maxwell-Boltzman distribution is sometimes parameterized using

      a

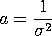
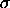      In scientific applications, the sigma parameter is typically parameterized in a way that has physical meaning.

      The Maxwell-Boltzman distribution can be generalized with location and scale parameters in the usual way. However, the scale parameter is not typically used since 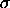sigma behaves much like a scale parameter already.

    Syntax:
      LET <y> = MAXCDF(<x>,<sigma>,<loc>,<scale>)
                              <SUBSET/EXCEPT/FOR qualification>
      where <x> is a variable or a parameter;
                  <sigma> is an optional number or parameter that specifies the value of the shape parameter;
                  <loc> is an optional number or parameter that specifies the value of the location parameter;
                  <scale> is an optional positive number or parameter that specifies the value of the scale parameter;
                  <y> is a variable or a parameter (depending on what <x> is) where the computed Maxwell-Boltzman cdf value is stored;
      and where the <SUBSET/EXCEPT/FOR qualification> is optional.

      If <sigma> is omitted, it defaults to 1. The location and scale parameters are optional.

    Examples:
      LET Y = MAXCDF(3)
      LET Y = MAXCDF(3,0.3)
      LET Y = MAXCDF(X1,SIGMA,MU)
      PLOT MAXCDF(X,SIGMA) FOR X = 0 0.01 5
    Default:
      None
    Synonyms:
      None
    Related Commands:
      MAXPDF = Compute the Maxwell probability density function.
      MAXPPF = Compute the Maxwell percent point function.
      CHPDF = Compute the chi probability density function.
      RAYPDF = Compute the Rayleigh probability density function.
      WEIPDF = Compute the Weibull probability density function.
      NORPDF = Compute the normal probability density function.
      LGNPDF = Compute the lognormal probability density function.
    Reference:
      "Continuous Univariate Distributions: Volume I", Second Edition, Johnson, Kotz, and Balakrishnan, Wiley, 1994, p. 451.
    Applications:
      Distributional Modeling, Statistical Physics
    Implementation Date:
      7/2004
    Program: 
       
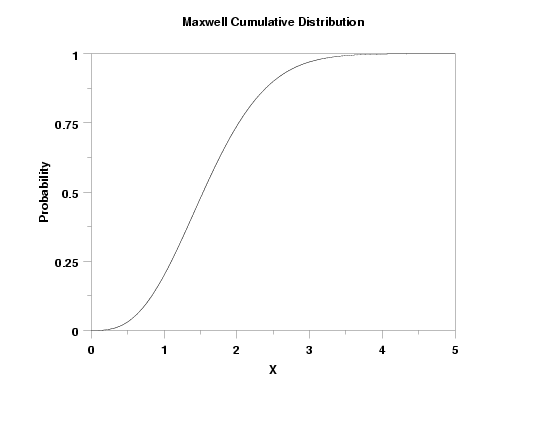
Y1LABEL Probability
X1LABEL X
LABEL CASE ASIS
TITLE CASE ASIS
TITLE Maxwell Cumulative Distribution
PLOT MAXCDF(X,1) FOR X = 0  0.01  5
      plot generated by sample program

    Date created: 7/28/2004
    Last updated: 7/28/2004
    Please email comments on this WWW page to alan.heckert@nist.gov.