PARTIAL CORRELATION MATRIX

PARTIAL CORRELATION MATRIX (LET)

Let Subcommand

Compute the partial correlation matrix of a matrix.

The partial correlation matrix computes the partial correlation coefficients of the columns of a matrix. That is, row i and column j of the partial correlation matrix is the partial correlation between column i and column j of the original matrix. This partial correlation between column i and column j is the correlation between these two columns after removing the effects of the remaining columns. Note that the diagonal elements of the partial correlation matrix will be 1 (since they are the partial correlation of a column with itself). The partial correlation matrix is also symmetric (since the partial correlation of column i with column j is the same as the partial correlation of column j with column i).

The algorithm for computing the partial correlations is:

1. Compute the standard correlation matrix.

2. Invert this correlation matrix.

3. Compute
   

   where r_ij is the (i,j)-th element of the inverted correlation matrix.

Alternatively, you can compute the CDF or the p-value for the partial correlation coefficients (i.e., to see if the partial correlation coefficient is significantly different than zero). The CDF value is

CDF = FCDF(VAL,1,N-NC)

where FCDF is the F cumulative distribution function with 1 and N - NC degrees of freedom (N is the number of observations and NC is the number of columns in the input matrix) and

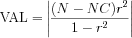
with r denoting the computed partial correlation. The pvalue is 1 - CDF.

LET <mat2> = PARTIAL CORRELATION MATRIX <mat1>
                        <SUBSET/EXCEPT/FOR qualification>
where <mat1> is a matrix for which the partial correlations are to be computed;
            <mat2> is a matrix where the resulting partial correlations are saved;
and where the <SUBSET/EXCEPT/FOR qualification> is optional and rarely used in this context.

LET <mat2> = PARTIAL CORRELATION CDF MATRIX <mat1>
                        <SUBSET/EXCEPT/FOR qualification>
where <mat1> is a matrix for which the partial correlation CDF's are to be computed;
            <mat2> is a matrix where the resulting partial correlation CDF's are saved;
and where the <SUBSET/EXCEPT/FOR qualification> is optional and rarely used in this context.

This syntax computes the CDF's of the partial correlation coefficients.

LET <mat2> = PARTIAL CORRELATION PVALUE MATRIX <mat1>
                        <SUBSET/EXCEPT/FOR qualification>
where <mat1> is a matrix for which the partial correlation p-value's are to be computed;
            <mat2> is a matrix where the resulting partial correlation p-values's are saved;
and where the <SUBSET/EXCEPT/FOR qualification> is optional and rarely used in this context.

This syntax computes the p-values of the partial correlation coefficients.

LET C = PARTIAL CORRELATION MATRIX A

By default, the partial correlation matrices are computed on the columns. That is, element (i,j) of the partial correlation matrix is the partial correlation between column i and column j of the input matrix.

To specify a partial correlation matrix based on rows rather than columns, enter the command

SET MATRIX CORRELATION DIRECTION ROW

To reset column based partial correlations, enter

SET MATRIX CORRELATION DIRECTION COLUMN

By default the Pearson correlation coefficient is computed. To specify a different type of correlation, enter the command
SET CORRELATION TYPE <DEFAULT/RANK/WINSORIZED/
            BIWEIGHT MIDCORRELATION/PERCENTAGE BEND/
            KENDALL TAU>

To see the definitions for these, enter

HELP RANK CORRELATION
HELP KENDALLS TAU
HELP BIWEIGHT MIDCORRELATION
HELP PERCENTAGE BEND

Matrices are created with either the READ MATRIX command or the MATRIX DEFINITION command. Enter HELP MATRIX DEFINITION and HELP READ MATRIX for details.

The columns of a matrix are accessible as variables by appending an index to the matrix name. For example, the 4x4 matrix C has columns C1, C2, C3, and C4. These columns can be operated on like any other DATAPLOT variable.

The maximum size matrix that DATAPLOT can handle is set when DATAPLOT is built on a particular site. The default maximums are 100 columns and 100 rows.

None

None

PARTIAL CORRELATION	= Compute the partial correlation of three variables.
CORRELATION MATRIX	= Generate the correlation matrix.
CORRELATION	= Compute the correlation of two variables.
RANK CORRELATION	= Compute the rank correlation of two variables.
KENDALLS TAU	= Compute the Kendall tau correlation of two variables.
WINSORIZED CORRELATION	= Compute the Winsorized correlation of two variables.
BIWEIGHT MIDCORRELATION	= Compute the biweight mid-correlation of two variables.
PERCENTAGE BEND CORRELATION	= Compute the percentage bend correlation of two variables.
COVARIANCE	= Compute the covariance of two variables.

Linear Fitting

2012/06

 
.  This data is from page 202 of
.
.  Peavy, Bremer, Varner, Hogben (1986), "OMNITAB 80:
.  An Interpretive System for Statistical and Numerical
.  Data Analysis," NBS Special Publication 701.
.
.  Original source of the data is from
.  Draper and Smith (1981), "Applied Regression Analysis",
.  Wiley, p. 373.
.
dimension 40 columns
.
read matrix m
42.2  11.2  31.9  167.1
48.6  10.6  13.2  174.4
42.6  10.6  28.7  160.8
39.0  10.4  26.1  162.0
34.7   9.3  30.1  140.8
44.5  10.8   8.5  174.6
39.1  10.7  24.3  163.7
40.1  10.0  18.6  174.5
45.9  12.0  20.4  185.7
end of data
.
set write decimals 4
let pcorr = partial correlation matrix m
print pcorr
    

The following output is generated.

        MATRIX PCORR   --            4 ROWS
                       --            4 COLUMNS

 VARIABLES--PCORR1         PCORR2         PCORR3         PCORR4  

         1.0000         0.4317        -0.4566         0.1054
         0.4317         1.0000         0.6972         0.7268
        -0.4566         0.6972         1.0000        -0.6478
         0.1054         0.7268        -0.6478         1.0000