

|
JSBCDFName:
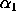 and and
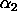 . .
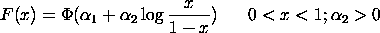
where
where <x> is a number, parameter, or variable containing values between 0 and 1; <y> is a variable or a parameter (depending on what <x> is) where the computed Johnson SB cdf values are stored; <alpha1> is a number, parameter, or variable that specifies the first shape parameter; <alpha2> is a number, parameter, or variable that specifies the second shape parameter; and where the <SUBSET/EXCEPT/FOR qualification> is optional.
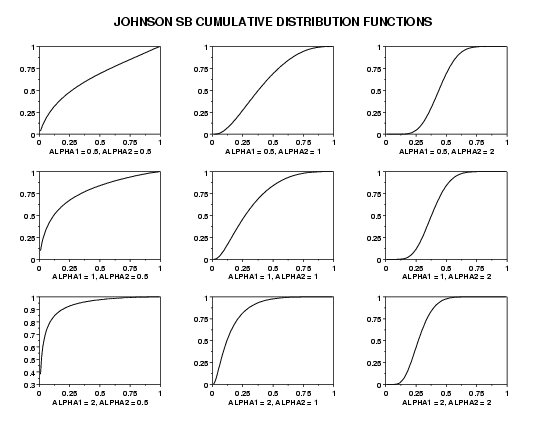
LET A = JSBCDF(A1,1.5,3) LET Y = JSBCDF(X,2,6) PLOT JSBCDF(X,0.8,2) FOR X = -5 0.1 20
LET ALPHA1 = DATA 0.5 0.5 0.5 1 1 1 2 2 2
LET ALPHA2 = DATA 0.5 1 2 0.5 1 2 0.5 1 2
.
MULTIPLOT 3 3
MULTIPLOT CORNER COORDINATES 0 0 100 95
LOOP FOR K = 1 1 9
LET A1 = ALPHA1(K)
LET A2 = ALPHA2(K)
X1LABEL ALPHA1 = ^A1, ALPHA2 = ^A2
PLOT JSBCDF(X,A1,A2) FOR X = 0.01 0.01 0.99
END OF LOOP
END OF MULTIPLOT
.
MOVE 50 97
HEIGHT 3
JUSTIFICATION CENTER
TEXT JOHNSON SB CUMULATIVE DISTRIBUTION FUNCTIONS
Date created: 11/20/2001 |