I0INT

I0INT (LET)

Library Function

This program computes the integral of the modified Bessel function I₀(x).

The I0INT function is defined as:

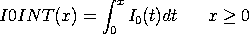
with I₀ denoting the modified Bessel function of the first kind of order 0.

Dataplot computes this function using ACM Algorithm 757 (see Reference: below). The function is computed using Chebyshev expansions, the coefficients of which are given to 20 decimal places.

LET <y> = I0INT(<x>)             <SUBSET/EXCEPT/FOR qualification>br> where <x> is a non-negative number, variable or parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed I0INT function values are stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = I0INT(2.3)
PLOT I0INT(X) FOR X = 0 .01 10
LET X2 = I0INT(X1) FOR X1 = 0.1 0.1 3.0

None

None

BESSI0	= Compute the modified Bessel function of the first kind and order 0.
BESSI1	= Compute the modified Bessel function of the first kind and order 1.
BESSIN	= Compute the modified Bessel function of the first kind and order N.
BESSJN	= Compute the Bessel function of the first kind and order N.
BESSKN	= Compute the modified Bessel function of the third kind and order N.
BESSYN	= Compute the Bessel function of the second kind and
J0INT	= Compute the integral of the Bessel function of the first kind and order 0.
K0INT	= Compute the integral of the modified Bessel function of the third kind and order 0.
Y0INT	= Compute the integral of the Bessel function of the second kind and order 0.
I0ML0	= Compute the difference of the modified Bessel function of the first kind of order 0 and the modified Struve function of order 0.
I1ML1	= Compute the difference of the modified Bessel function of the first kind of order 1 and the modified Struve function of order 1.

"ACM Transactions of Mathematical Software", Allan MacLead, Vol. 22, No. 3, September, 1996, pp. 288-301.

Special Functions

2005/11

 
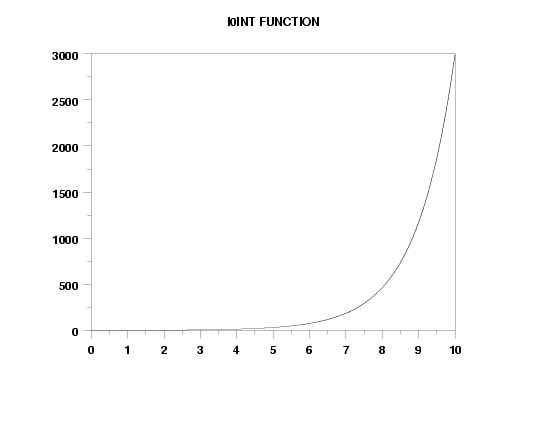
TITLE I0INT FUNCTION
PLOT I0INT(X) FOR X = 0 0.01 10