GL3PDF

GL3PDF (LET)

Library Function

Compute the type 3 generalized logistic probability density function with shape parameter .

The standard form of the type 3 generalized logistic distribution has the probability density function:

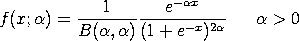
The general form of the type 3 generalized logistic probability density function can be obtained by replacing x in the above formula with (x-loc)/scale.

LET <y> = GL3PDF(<x>,<alpha>,<loc>,<scale>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a variable, number or parameter;
            <alpha> is a number or parameter that specifies the value of the shape parameter;
            <loc> is a number or parameter that specifies the value of the location parameter;
            <scale> is a number or parameter that specifies the value of the scale parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed generalized logistic type 3 pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

The location and scale parameters are optional.

LET A = GL3PDF(3,2)
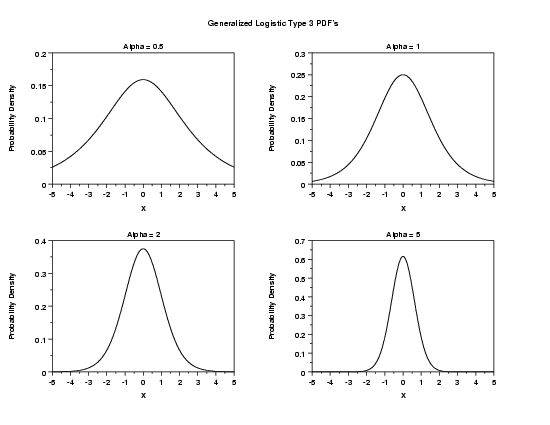
LET X2 = GL3PDF(X1,ALPHA)
PLOT GL3PDF(X,ALPHA) FOR X = -5 0.01 5

The generalized logistic type 3 distribution is symmetric for all values of . A value of = 1 results in the logistic distribution. Values of < 1 result in in heavier tails than the logistic distribution while values of > 1 result in shorter tails than the logistic distribution.

Generalized logistic type 3 random numbers, probability plots, and goodness of fit tests can be generated with the commands:
LET ALPHA = <value>
LET Y = GENERALIZED LOGISTIC TYPE 3 RANDOM NUMBERS ...
            FOR I = 1 1 N
GENERALIZED LOGISTIC TYPE 3 PROBABILITY PLOT Y
GENERALIZED LOGISTIC TYPE 3 KOLMOGOROV SMIRNOV ...
            GOODNESS OF FIT Y
GENERALIZED LOGISTIC TYPE 3 CHI-SQUARE ...
            GOODNESS OF FIT Y


The following commands can be used to estimate the shape parameter for the generalized logistic type 3 distribution:

LET ALPHA1 = <value>
LET ALPHA2 = <value>
GENERALIZED LOGISTIC TYPE 3 PPCC PLOT Y
GENERALIZED LOGISTIC TYPE 3 KS PLOT Y


The default values for ALPHA1 and ALPHA2 are 0.1 and 3, respectively.

Johnson, Kotz, and Balakrishnan (see Reference section below) also define type 1, type 3, type 4, and a parameterization due to Hoskings generalized logistic distributions. These are also supported by Dataplot (see the Related Commands section below).

None

None

GL3CDF	= Compute the generalized logistic type 3 cumulative distribution function.
GL3PPF	= Compute the generalized logistic type 3 percent point function.
GLOPDF	= Compute the generalized logistic type 1 probability density function.
GL2PDF	= Compute the generalized logistic type 2 probability density function.
GL4PDF	= Compute the generalized logistic type 4 probability density function.
GL5PDF	= Compute the generalized logistic (Hosking parameterization) probability density function.
LOGPDF	LOGPDF = Compute the logistic probability density function.
NORPDF	= Compute the normal probability density function.
LGNPDF	= Compute the logmormal probability density function.

"Continuous Univariate Distributions - 2", 2nd. Ed., Johnson, Kotz, and Balakrishnan, John Wiley, 1994 (pp. 140-147).

Distributional Modeling

2006/3

LET A = DATA 0.5  1  2  5
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
LABEL CASE ASIS
TITLE CASE ASIS
TITLE DISPLACEMENT 2
X1LABEL X
Y1LABEL Probability Density
X1LABEL DISPLACEMENT 12
Y1LABEL DISPLACEMENT 15
.
LOOP FOR K = 1 1 4
   LET ALPHA = A(K)
   TITLE Alpha = ^ALPHA
   PLOT GL3PDF(X,ALPHA) FOR X = -5  0.01  5
END OF LOOP
END OF MULTIPLOT
CASE ASIS
MOVE 50 97
JUSTIFICATION CENTER
TEXT Generalized Logistic Type 3 PDF's