GGDCHAZ

GGDCHAZ (LET)

Library Function

Compute the standard form of the generalized gamma cumulative hazard function.

The standard form of the generalized gamma distribution has the following cumulative hazard function:

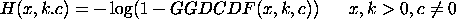
where k and c are shape parameters and GGDCDF is the cumulative distribution function of the generalized gamma distribution.

LET <y> = GGDCHAZ(<x>,<k>,<c>)             <SUBSET/EXCEPT/FOR qualification>
where <x> is a positive number, parameter, or a variable;
            <y> is a variable or a parameter (depending on what <x> is) where the computed generalized gamma cumulative hazard value is saved;
            <k> is a positive number, parameter, or variable that specifies the first shape parameter;
            <c> is a non-zero number, parameter, or variable that specifies the second shape parameter;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = GGDCHAZ(3,1.5.0.6)
LET X2 = GGDCHAZ(X1,GAMMA,POWER)

If c is 1, this distribution reduces to the standard gamma distribution. If k is 1, this distribution reduces to a Weibull distribution. If k =1/2 and c = 2, it reduces to a half-normal distribution. Several other common distributions are special cases of the generalized gamma distribution.

The second shape parameter can be negative (but not zero). Specifically, if c = -1, the generalized gamma reduces to the inverted gamma distribution.

None

None

GGDCDF	= Compute the generalized gamma cumulative distribution function.
GGDPDF	= Compute the generalized gamma probability density function.
GGDPPF	= Compute the generalized gamma percent point function.
GGDHAZ	= Compute the generalized gamma hazard function.
GAMPDF	= Compute the gamma probability density function.
IGAPDF	= Compute the inverted gamma probability density function.
WEIPDF	= Compute the Weibull probability density function.
EXPPDF	= Compute the exponential probability density function.
CHSPDF	= Compute the chi-square probability density function.

"Continuous Univariate Distributions", 2nd. ed., Johnson, Kotz, and Balakrishnan, John Wiley and Sons, 1994 (chapter 17).

"Statistical Distributions", 2nd. Edition, Evans, Hastings, and Peacock, Wiley and Sons, 1993 (chapter 18).

Reliability

98/4

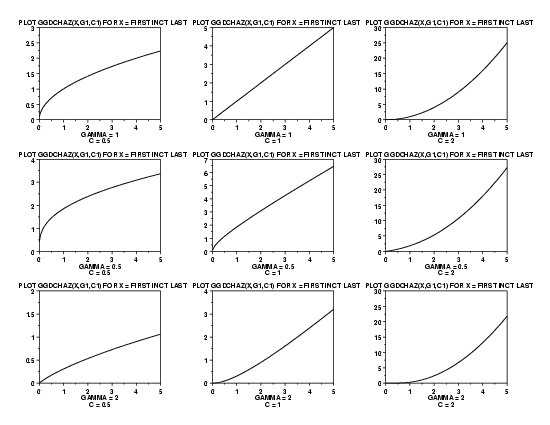
    LET G = DATA 1 1 1 0.5 0.5 0.5 2 2 2 
    LET C = DATA 0.5 1 2 0.5 1 2 0.5 1 2 
    LET START = DATA 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 
    LET INC = DATA 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 
    LET STOP = DATA 5 5 5 5 5 5 5 5 5 
    . 
    MULTIPLOT 3 3; MULTIPLOT CORNER COORDINATES 0 0 100 100 
    TITLE AUTOMATIC 
    LOOP FOR K = 1 1 9 
       LET G1 = G(K) 
       LET C1 = C(K) 
       LET FIRST = START(K) 
       LET LAST = STOP(K) 
       LET INCT = INC(K) 
       X1LABEL GAMMA = ^G1 
       X2LABEL C = ^C1 
       PLOT GGDCHAZ(X,G1,C1) FOR X = FIRST INCT LAST 
    END OF LOOP 
    END OF MULTIPLOT