ERRPPF

ERRPPF (LET)

Library Function

Compute the standard error probability density function. This is also referred to as the exponential power distribution, the Subbotin distribution, or the general error distribution.

Dataplot supports another distribution that is also called the exponential power distribution. This is a different distribution than the one described here (enter HELP PEXPDF for details).

Note that there are several different parameterizations of the error distribution in the literature. We will use the parameterization of Radikamalla (see the Reference section below).

The standard error distribution has the following probability density function:

with and denoting the gamma function (HELP GAMMA for details) and the shape parameter, respectively.

The error percent point function is computed by numerically inverting the cumulative distribution function using a bisection method. For = 1 and = 2, the percent point functions for the double exponential and normal distributions, respectively, are used.

For = 1 and = 2, the error distribution is equivalent to the double exponential and normal distribution, respectively. As goes to infinity, the error distribution approximates a uniform distribution. For applications, values of between 1 and 6 are typically of most interest. The error distribution is sometimes used in simulation studies because it provides a symmetric distribution with widely varying kurtosis.

The error distribution can be generalized with location and scale parameters in the usual way.

LET <y> = ERRPDF(<p>,<alpha>,<loc>,<scale>)
                        <SUBSET/EXCEPT/FOR qualification>
where <p> is a variable, a number, or a parameter in the interval (0,1);
            <alpha> is a number or parameter specifying the shape parameter;
            <loc> is a number or parameter that specifies the value of the location parameter;
            <scale> is a number or parameter that specifies the value of the scale parameter;
            <y> is a variable or a parameter (depending on what <p> is) where the computed error ppf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

Note that the location and scale parameters are optional.

LET A = ERRPPF(0.95,2)
LET X2 = ERRPPF(P1,A)
PLOT ERRPPF(P,1.5) FOR X = 0.01 0.01 0.99

None

None

ERRCDF	= Compute the error cumulative distribution function.
ERRPDF	= Compute the error probability density function.

"Random Sampling From the Exponential Power Distribution", Pandu R. Radikamalla, Journal of the American Statistical Association, September, 1980, pp. 683-686.

"Statistical Distributions", Third Edition, Evans, Hastings, and Peacock, Wiley, 2000.

"Continuous Univariate Distributions--Volume 2, Second Edition", Johnson, Kotz, and Balakrishnan, Wiley, 1994.

Distributional Modeling

2003/5

 
X1LABEL Probability
Y1LABEL X
LABEL CASE ASIS
X1LABEL DISPLACEMENT 12
Y1LABEL DISPLACEMENT 12
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 100
MULTIPLOT SCALE FACTOR 2
TITLE AUTOMATIC
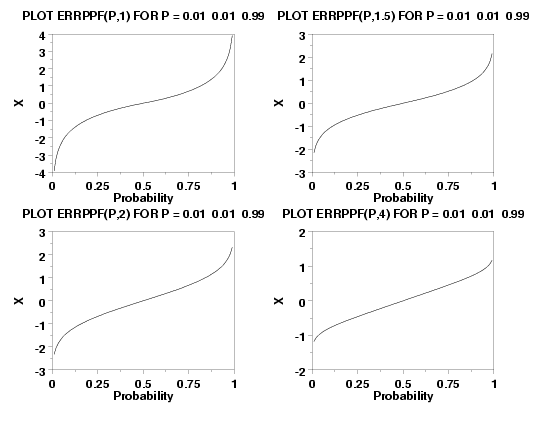
PLOT ERRPPF(P,1) FOR P = 0.01  0.01  0.99
PLOT ERRPPF(P,1.5) FOR P = 0.01  0.01  0.99
PLOT ERRPPF(P,2) FOR P = 0.01  0.01  0.99
PLOT ERRPPF(P,4) FOR P = 0.01  0.01  0.99
END OF MULTIPLOT