SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

DIFFERENCE OF PROPORTION HYPOTHESIS TEST

Name:
    DIFFERENCE OF PROPORTION HYPOTHESIS TEST (LET)
Type:
    LET Subcommand
Purpose:
    Return the p-value for a large sample hypothesis test for the equality of two binomial proportions.
Description:
    Given a set of N1 observations in a variable X1 and a set of N2 observations in a variable X2, we can compute a normal approximation test that the two proportions are equal (or alternatively, that the difference of the two proportions is equal to 0). In the following, let p1 and p2 be the population proportion of successes for samples one and two, respectively.

    The hypothesis test that the two binomial proportions are equal is

      H0: p1 = p2
      Ha: p1 ≠ p2
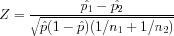
      Test Statistic: Z = (p1hat - p2hat)/SQRT(phat*(1-phat)*((1/n1) + (1/n2)))

      where phat is the proportion of successes for the combined sample and

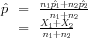
      phat = (n1*p1hat + n2*phat2)/(n1 + n2) = (x1 + x2)/(n1 + n2)

      Significance Level: alpha
      Critical Region: For a two-tailed test

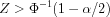
      Z > NORPPF(1 - alpha/2)
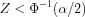
      Z < NORPPF(alpha/2)

      For a lower tailed test

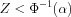
      Z < NORPPF(alpha)

      For an upper tailed test

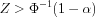
      Z > NORPPF(1 - alpha)

      Conclusion: Reject the null hypothesis if Z is in the critical region

    For a lower tailed test, the p-value is equal to NORCDF(Z). For an upper tailed test, the p-value is equal to 1 - NORCDF(Z). For a two-tailed test, the p-value is equal to 2*(1 - NORCDF(Z)).

    Alternatively, you can request that the lower and upper confidence limits for p1 - p2 be returned instead of the p-value for the hypothesis test.

Syntax 1:
    LET PVAL = DIFFERENCE OF PROPORTION HYPOTHESIS TEST <p1> <n1> <p2> <n2> <alpha> where <p1> is a parameter that specifies the proportion of successes for sample 1; <n1> is a parameter that specifies the sample size for sample 1; <p2> is a parameter that specifies the proportion of successes for sample 2; <n2> is a parameter that specifies the sample size for sample 2; <alpha> is a parameter that specifies the desired significance level; and <pval> is the returned p-value.
This syntax is used for the two-tailed case. Syntax 2:
    LET PVAL = DIFFERENCE OF PROPORTION LOWER TAIL HYPOTHESIS TEST <p1> <n1> <p2> <n2> <alpha> where <p1> is a parameter that specifies the proportion of successes for sample 1; <n1> is a parameter that specifies the sample size for sample 1; <p2> is a parameter that specifies the proportion of successes for sample 2; <n2> is a parameter that specifies the sample size for sample 2; <alpha> is a parameter that specifies the desired significance level; and <pval> is the returned p-value.
This syntax is used for the lower tailed case. Syntax 3:
    LET PVAL = DIFFERENCE OF PROPORTION UPPER TAIL HYPOTHESIS TEST <p1> <n1> <p2> <n2> <alpha> where <p1> is a parameter that specifies the proportion of successes for sample 1; <n1> is a parameter that specifies the sample size for sample 1; <p2> is a parameter that specifies the proportion of successes for sample 2; <n2> is a parameter that specifies the sample size for sample 2; <alpha> is a parameter that specifies the desired significance level; and <pval> is the returned p-value.
This syntax is used for the upper tailed case. Syntax 4:
    LET <al> <au> = DIFFERENCE OF PROPORTION CONFIDENCE LIMITS <p1> <n1> <p2> <n2> <alpha> where <p1> is a parameter that specifies the proportion of successes for sample 1; <n1> is a parameter that specifies the sample size for sample 1; <p2> is a parameter that specifies the proportion of successes for sample 2; <n2> is a parameter that specifies the sample size for sample 2; <alpha> is a parameter that specifies the desired significance level; <al> is the returned lower confidence limit; and <au> is the returned upper confidence limit.
This syntax is used for the two-tailed case. Examples:
    DIFFERENCE OF PROPORTION HYPOTHESIS TEST Y1 Y2
    DIFFERENCE OF PROPORTION HYPOTHESIS TEST P1 N1 P2 N2

Note:
    The BINOMIAL PROPORTION TEST generates this test with full output.
Default:
    None
Synonyms:
    None
Related Commands:
References: NIST/SEMATECH e-Handbook of Statistical Methods, http://www.itl.nist.gov/div898/handbook/prc/section3/prc33.htm. Ryan (2008), "Modern Engineering Statistics", Wiley, pp. 124-126. Applications:
    Categorical Data Analysis
Implementation Date:
    2008/8
Program 1:
    LET X1 = 32 LET N1 = 38 LET P1 = X1/N1 LET X2 = 39 LET N2 = 44 LET P2 = X1/N1 LET ALPHA = 0.05 LET PVAL = DIFFERENCE OF PROPORTION HYPOTHESIS TEST P1 N1 P2 N2

    plot generated by sample program

Date created: 1/26/2009
Last updated: 1/26/2009
Please email comments on this WWW page to alan.heckert@nist.gov.