DIFFERENCE OF AAD

DIFFERENCE OF AAD (LET)

Let Subcommand

Compute the difference between the average absolute deviations (AAD) for two response variables.

The average absolute deviation is defined as
\( AAD = \frac{\sum_{i=1}^{n}{|x - \bar{x}|}}{n} \)

with \( \bar{x} \) denoting the mean of the variable and n denoting the number of observations. This statistic is sometimes used as an alternative to the standard deviation.

For the difference of average absolute deviations, the average absolute deviation is computed for each of two samples then their difference is taken.

LET <par> = DIFFERENCE OF AAD <y1> <y2>             <SUBSET/EXCEPT/FOR qualification>
where <y1> is the first response variable;
            <y2> is the first response variable;
            <par> is a parameter where the computed difference of the average absolute deviations is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = DIFFERENCE OF AAD Y1 Y2
LET A = DIFFERENCE OF AAD Y1 Y2 SUBSET X > 1

Prior to the 2014/07 version, the AVERAGE ABSOLUTE DEVIATION command computed the difference from the median rather than the mean. The 2014/07 version corrected this command to compute differences from the mean and added the command
AVERAGE ABSOLUTE DEVIATION FROM THE MEDIAN

to compute differences from the median.

Since the DIFFERENCE OF AVERAGE ABSOLUTE DEVIATIONS was based on the average absolute deviation computation, these changes apply to it as well.

Dataplot statistics can be used in a number of commands. For details, enter
HELP STATISTICS

None

AVERAGE ABSOLUTE DEVIATION is a synonym for AAD.

AVERAGE ABSOLUTE DEVIATION	=	Compute the absolute average deviation from the mean of a variable.
AVERAGE ABSOSOLUTE DEVIATION FROM THE MEDIAN	=	Compute the average absolute deviation from the median of a variable.
MEDIAN ABSOLUTE DEVIATION	=	Compute the median absolute deviation of a variable.
STANDARD DEVIATION	=	= Compute the standard deviation of a variable.
VARIANCE	=	Compute the variance of a variable.
RANGE	=	Compute the range of a variable.

Data Analysis

3/2002

SKIP 25 
READ IRIS.DAT Y1 TO Y4 X 
. 
LET A = DIFFERENCE OF AAD Y1 Y2 
TABULATE DIFFERENCE OF AAD Y1 Y2 X 
. 
XTIC OFFSET 0.2 0.2 
X1LABEL GROUP ID 
Y1LABEL DIFFERENCE OF AAD 
CHAR X 
LINE BLANK 
DIFFERENCE OF AAD PLOT Y1 Y2 X 
CHAR X ALL 
LINE BLANK ALL 
BOOTSTRAP DIFFERENCE OF AAD PLOT Y1 Y2 X  
    

Dataplot generated the following output.

       ***************************************
       **  LET A = DIFFERENCE OF AAD Y1 Y2  **
       ***************************************
  
  
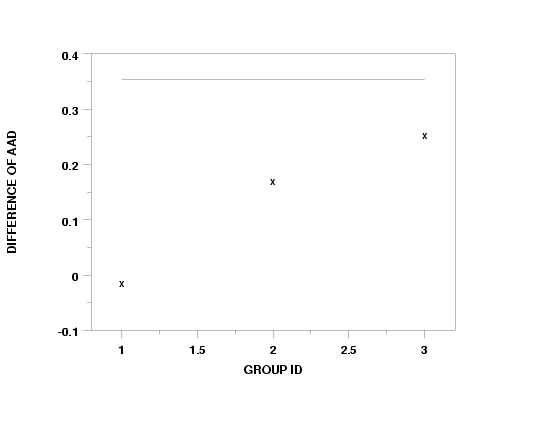
 THE COMPUTED VALUE OF THE CONSTANT A             =  0.35400003E+00
  
  
       ******************************************
       **  TABULATE DIFFERENCE OF AAD Y1 Y2 X  **
       ******************************************
  
  
                 *    Y1       AND Y2
     X           *    DIFFERENCE OF AVERAGE ABSOLUTE
 **********************************************
     1.00000     *   -0.140000E-01
     2.00000     *    0.170000
     3.00000     *    0.254000
  
       GROUP-ID AND STATISTIC WRITTEN TO FILE DPST1F.DAT