BIWEIGHT LOCATION

BIWEIGHT LOCATION (LET)

Let Subcommand

Compute a biweight based location estimate for a variable.

Mosteller and Tukey (see Reference section below) define two types of robustness:
1. resistance means that changing a small part, even by a large amount, of the data does not cause a large change in the estimate

2. robustness of efficiency means that the statistic has high efficiency in a variety of situations rather than in any one situation. Efficiency means that the estimate is close to optimal estimate given that we distribution that the data comes from. A useful measure of efficiency is:
   Efficiency = (lowest variance feasible)/(actual variance)

Many statistics have one of these properties. However, it can be difficult to find statistics that are both resistant and have robustness of efficiency.

For location estimaors, the mean is the optimal estimator for Gaussian data. However, it is not resistant and it does not have robustness of efficiency. The median is a resistant estimate, but it has only moderate robustness of efficiency.

The biweight location estimator is both resistant and robust of efficiency. Mosteller and Tukey recommend using the median for exploratory work where moderate efficiency in a variety of situations is adequate and the biweight in situations when high performance is needed.

The biweight location estimate is defined as:

\( y* = \frac{\sum_{i=1}^{n}{w_{i}y_{i}}} {\sum_{i=1}^{n}{w_{i}}} \)

where

\( w_{i} = (1 - (\frac{y_{i} - y*}{cS})^{2})^{2} \hspace{0.5in} \mbox{for } (\frac{y_{i} - y*}{cS})^{2} < 1 \)

\( w_{i} = 0 \hspace{0.5in} \mbox{otherwise} \)

and

\( S = \mbox{median}\{|y_{i} - y*|\} \)

c = 6 (using 6 means that residuals up to approximately \( 4 \sigma \) are included)

Note that this is an iterative estimate since y* depends on w_i and w_i depends on y*.

Dataplot will compute up to 10 iterations (computation is terminated if the biweight location estimate does not change in value by more than 0.000001).

LET <par> = BIWEIGHT LOCATION <y>           <SUBSET/EXCEPT/FOR qualification>
where <y> is the response variable;
          <par> is a parameter where the computed biweight location is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = BIWEIGHT LOCATION Y1
LET A = BIWEIGHT LOCATION Y1 SUBSET TAG > 2

Dataplot statistics can be used in a number of commands. For details, enter
HELP STATISTICS

None

None

BIWEIGHT SCALE	= Compute a biweight scale estimate of a variable.
BIWEIGHT CONFIDENCE LIMITS	= Compute a biweight based confidence interval.
MEAN	= Compute the mean of a variable.
MEDIAN	= Compute the median of a variable.
MIDMEAN	= Compute the midmean of a variable.
TRIMMED MEAN	= Compute the trimmed mean of a variable.
WINSORIZED MEAN	= Compute the Winsorized mean of a variable.
AVERAGE ABSOLUTE DEVIATION	= Compute the average absolute deviation of a variable.
MEDIAN ABSOLUTE DEVIATION	= Compute the median absolute deviation of a variable.
STANDARD DEVIATION	= Compute the standard deviation of a variable.

Mosteller and Tukey (1977), "Data Analysis and Regression: A Second Course in Statistics," Addison-Wesley, pp. 203-209.

Robust Data Analysis

2001/11

    LET Y1 = NORMAL RANDOM NUMBERS FOR I = 1 1 10000
    LET Y2 = LOGISTIC RANDOM NUMBERS FOR I = 1 1 10000
    LET Y3 = CAUCHY RANDOM NUMBERS FOR I = 1 1 10000
    LET Y4 = DOUBLE EXPONENTIAL RANDOM NUMBERS FOR I = 1 1 10000
    LET A1 = BIWEIGHT LOCATION Y1
    LET A2 = BIWEIGHT LOCATION Y2
    LET A3 = BIWEIGHT LOCATION Y3
    LET A4 = BIWEIGHT LOCATION Y4
    LET B1 = MEAN Y1
    LET B2 = MEAN Y2
    LET B3 = MEAN Y3
    LET B4 = MEAN Y4
    LET C1 = MEDIAN Y1
    LET C2 = MEDIAN Y2
    LET C3 = MEDIAN Y3
    LET C4 = MEDIAN Y4
    PRINT "BIWEIGHT LOCATION ESTIMATE FOR NORMAL      RANDOM NUMBERS = ^A1"
    PRINT "MEAN              ESTIMATE FOR NORMAL      RANDOM NUMBERS = ^B1"
    PRINT "MEDIAN            ESTIMATE FOR NORMAL      RANDOM NUMBERS = ^C1"
    PRINT " "
    PRINT "BIWEIGHT LOCATION ESTIMATE FOR LOGISTIC    RANDOM NUMBERS = ^A2"
    PRINT "MEAN              ESTIMATE FOR LOGISTIC    RANDOM NUMBERS = ^B2"
    PRINT "MEDIAN            ESTIMATE FOR LOGISTIC    RANDOM NUMBERS = ^C2"
    PRINT " "
    PRINT "BIWEIGHT LOCATION ESTIMATE FOR CAUCHY      RANDOM NUMBERS = ^A3"
    PRINT "MEAN              ESTIMATE FOR CAUCHY      RANDOM NUMBERS = ^B3"
    PRINT "MEDIAN            ESTIMATE FOR CAUCHY      RANDOM NUMBERS = ^C3"
    PRINT " "
    PRINT "BIWEIGHT LOCATION ESTIMATE FOR DOUBLE EXPO RANDOM NUMBERS = ^A4"
    PRINT "MEAN              ESTIMATE FOR DOUBLE EXPO RANDOM NUMBERS = ^B4"
    PRINT "MEDIAN            ESTIMATE FOR DOUBLE EXPO RANDOM NUMBERS = ^C4"
    

Dataplot generates the following output:

    BIWEIGHT LOCATION ESTIMATE FOR NORMAL      RANDOM NUMBERS = 0.001006
    MEAN              ESTIMATE FOR NORMAL      RANDOM NUMBERS = 0.005167
    MEDIAN            ESTIMATE FOR NORMAL      RANDOM NUMBERS = -0.01028
     
    BIWEIGHT LOCATION ESTIMATE FOR LOGISTIC    RANDOM NUMBERS = -0.0074
    MEAN              ESTIMATE FOR LOGISTIC    RANDOM NUMBERS = 0.000867
    MEDIAN            ESTIMATE FOR LOGISTIC    RANDOM NUMBERS = 0.016679
     
    BIWEIGHT LOCATION ESTIMATE FOR CAUCHY      RANDOM NUMBERS = -0.00439
    MEAN              ESTIMATE FOR CAUCHY      RANDOM NUMBERS = 3.70155
    MEDIAN            ESTIMATE FOR CAUCHY      RANDOM NUMBERS = -0.01582
     
    BIWEIGHT LOCATION ESTIMATE FOR DOUBLE EXPO RANDOM NUMBERS = -0.00203
    MEAN              ESTIMATE FOR DOUBLE EXPO RANDOM NUMBERS = -0.00723
    MEDIAN            ESTIMATE FOR DOUBLE EXPO RANDOM NUMBERS = -0.00557
    

 
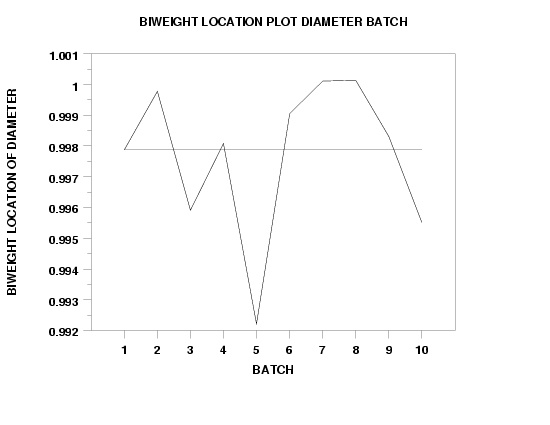
    SKIP 25
    READ GEAR.DAT DIAMETER BATCH
    TITLE AUTOMATIC
    XLIMITS 1 10
    MAJOR XTIC MARK NUMBER 10
    MINOR XTIC MARK NUMBER 0
    XTIC OFFSET 1 1
    X1LABEL BATCH
    Y1LABEL BIWEIGHT LOCATION OF DIAMETER
    BIWEIGHT LOCATION PLOT DIAMETER BATCH
    

 
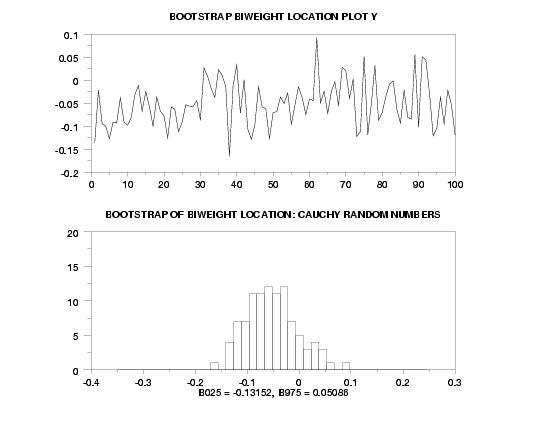
    MULTIPLOT 2 1
    MULTIPLOT CORNER COORDINATES 0 0 100 100
    LET Y = CAUCHY RANDOM NUMBERS FOR I = 1 1 1000
    TITLE AUTOMATIC
    BOOTSTRAP BIWEIGHT LOCATION PLOT Y
    X1LABEL B025 = ^B025, B975 = ^B975
    TITLE BOOTSTRAP OF BIWEIGHT LOCATION: CAUCHY RANDOM NUMBERS
    HISTOGRAM YPLOT
    END OF MULTIPLOT