SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 1 Vol 2

BEST CP

Name:
    BEST CP
Type:
    Analysis Command
Purpose:
    Performs a best CP analysis.
Description:
    In multilinear regression, a common task is to determine the "best" set of independent variables to use in the fit. There are three basic approaches to this problem:

    1. Perform all regressions and pick the best candidate models from this list. This is called "all subsets" regression.

    2. Start with the independent variable that provides the best fit for models containing only one independent variable. Then at each step, add one more independent variable from the remaining variables that provides the most improvement in the fit. Continue until adding an additional variable results in no significant improvement in the model. This is called "forward stepwise" regression.

    3. "Backward stepwise" regression is similar to forward stepwise regression. However, instead of starting with one independent variable and adding one at each stage, the initial model contains all the independent variable. Then one variable is deleted at each stage until the best model is reached.

    There can be some variations in the above approaches. For example,

    1. Different critierion have been proposed for deciding which variable to add/delete at a given step in forward/backward stepwise regression.

    2. Different criterion have been proposed for deciding when to quit adding/deleting variables in forward/backward stepwise regression.

    3. Some algorithms allow an entered variable to be removed at a later step.

    The choice of these critierion is complicated by the fact that adding additional variables will always increase the R2 of the fit (or at least not decrease it). However, including too many variables increases multicolinearity which results in numerically unstable models (i.e., you are essentially fitting noise). In addition, the model becomes more complex than it needs to be. A number of critierion have been proposed that attempt to balance maximizing the fit while trying to protect against overfitting.

    All subsets regression is the preferred algorithm in that it examines all models. However, it can be computationally impractical to perform all subsets regression when the number of independent variables becomes large. The primary disadvantage of forward/backward stepwise regression is that it may miss good candidate models. Also, they pick a single model rather than a list of good candidate models that can be examined closer.

    Dataplot addresses this issue with the BEST CP command. This is based on the following:

    1. It implements the "leaps and bounds" algorithm of Furnival and Wilson (see reference below). This algorithm is a compromise between all subsets regression and forward/backward stepwise regression. It provides an efficient algorithm for identifying the best candidate models without actually computing all possible models. It thus provides the advantage of all subset regressions (i.e., all potential models are included) while remaining computationally practical for a large number of indpendent variables.

    2. Dataplot uses the Mallow's Cp critierion (suggested by Mallows, see References below). The Cp statistic is defined as follows:

        \( C_{p} = \frac{RSS_{p}}{\hat{\sigma}^2} + 2p - n \)

      where

        n = the number of observations
        p = the number of coefficents in the regression
        RSSp = the residual sum of squares for the reduced model
        \( \hat{\sigma} \) = an independent estimate of the error (although this value is typically unknown, it is estimated using the residual variance from the full model)

      If the model is satisfactory, Cp will be approximately equal to p.

    It should be emphasized that the BEST CP command is intended simply to identify good candidate models. Also, the BEST CP command uses a computationally fast algorithm that is not as accurate as the algorithm used by the FIT command. The FIT command should be applied to identified models that are of interest. Also, standard regression diagnostics should be examined to the candidate models of interest.

Syntax:
    BEST CP <y> <x1> ... <xk>               <SUBSET/EXCEPT/FOR qualification>
    where <y> is the response (dependent) variable;
                  <x1> .... <xk> is a list of one or more independent variables;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
    BEST CP Y X1 X2 X3 X4 X5 X6 X7
    BEST CP Y X1 X2 X3 X4 X5 X6 X7 SUBSET TAG > 1
Note:
    The BEST CP commands requires at least three indpendent variables and at most 38 independent variables.
Note:
    By default, the BEST CP command returns the 10 best candidate models (7 if there only three independent variables). Note that more than 10 may actually be returned. This is due to the fact that additional models may be "free" in the leaps and bounds computations.

    To change the number of candidate models chosen, enter the command

      SET NUMBER OF CP <value>

    where <value> identifies the number of candidate models.

    Note that increasing <value> will result in greater time to generate the best candidate models. In most cases, the default value of 10 is adequate.

Note:
    It can be helpful to plot the results of the BEST CP command.

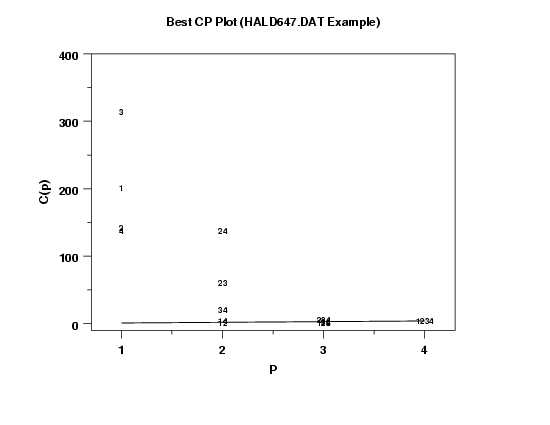
    Dataplot writes the results of the CP analysis to file. The example program below shows how to generate a CP plot using these files. Specifically,

    1. The Cp statistic and the corresponding model is written to "dpst1f.dat". The following is a sample dpst1f.dat file: 
        1 138.731 : X4
1 142.487 : X2
1 202.549 : X1
1 315.155 : X3
2   2.678 : X1       X2
2   5.496 : X1       X4
2  22.373 : X3       X4
2  62.438 : X2       X3
2 138.226 : X2       X4
3   3.018 : X1       X2       X4
3   3.041 : X1       X2       X3
3   3.497 : X1       X3       X4
3   7.338 : X2       X3       X4
4   5.000 : X1       X2       X3       X4
    2. A coded form of the model is written to the file "dpst2f.dat". This coded form is useful as an identifying plot character in a CP plot. The rows of dpst1f.dat correspond to the rows of dpst2f.dat. The following is a sample dpst2f.dat file: 
        4
2
1
3
12
14
34
23
24
124
123
134
234
1234
Note:
    Dataplot uses code from OMNITAB to implement the BEST CP comamnd. The OMNITAB algorithm is based on the Furnival and Wilson leaps and bounds algorithm.
Note:
    The Mallows CP statistic can be affected by outliers. This is discussed by Ryan (see References below). Currently, Dataplot makes no provisions for outliers in the BEST CP command.
Note:
    Akaike introduced the concept of information criterion for model selection. Information criterion are based on penalizing the likelihood based on the number of parameters in the model. Akaike's original formulation is referred to as AIC (Akaike Information Critierion) and has been shown to be equivalent to Mallow's CP in the case of linear regression by Boisbunon, Canu, Fourdrinier, Strawderman, and Wells (2013).

    Schwarz introduced an alternative information critierion called the Bayesian Information Critierion (BIC). The BIC penalizes the likelihood more than the AIC for additional parameters. For large n, the BIC can be approximated by

      \( \mbox{BIC} = -2 \log(\hat{L}) + k \log(n) \)

    \(\hat{L}\) is the maximized value of the likelihood function. In the context of regression, the BIC can be computed as

      \( \mbox{BIC} = n \log(\mbox{resvar}) + k \log(n) \)

    where

      n = sample size
      k = the number of estimated coefficients
      resvar = \( \frac{\sum_{i=1}^{n}{(Y_{i} - Y_{\mbox{pred}})^2}} {n} \)

    The 2013/10 version of Dataplot added the BIC value for the selected models to the output. Note that the models are selected on the basis of Mallow's CP, not BIC. BIC is provided as an additional comparison.

Default:
    10 candidate models are extracted
Synonyms:
    None
Related Commands: Reference:
    Furnival and Wilson (1974), "Regression by Leaps and Bounds," Technometrics, Vol. 16, No. 4.

    C. L. Mallows (1966), "Choosing a Subset Regression," Joint Statistical Meetings, Los Angeles, CA.

    Sally Peavy, Shirley Bremer, Ruth Varner, and David Hogben (1986), "OMNITAB 80: An Interpretive System for Statistical and Numerical Data Analysis," NIST Special Publication 701.

    Thomas Ryan (1997), "Modern Regresion Methods," John Wiley, pp. 223-228.

    Schwarz (1978), "Estimating the dimension of a model," Annals of Statistics, Vol. 6, No. 2, pp. 461–464.

    Boisbunon, Canu, Fourdrinier, Strawderman, and Wells (2013), "AIC and Cp as estimators of loss for spherically symmetric distributions," arXiv:1308.2766.

Applications:
    Multilinear Fitting
Implementation Date:
    2002/7
    2013/10: Reformatted output
    2013/10: Added BIC values to output
Program: 
     
skip 25
read hald647.dat y x1 x2 x3 x4
.
echo on
capture junk.dat
best cp y x1 x2 x3 x4
end of capture
.
skip 0
read dpst1f.dat p cp
read row labels dpst2f.dat
title case asis
label case asis
character rowlabels
line blank
tic offset units data
xtic offset 0.3 0.3
ytic offset 10 0
let maxp = maximum p
major xtic mark number maxp
xlimits 1 maxp
title Best CP Plot (HALD647.DAT Example)
x1label P
y1label C(p)
plot cp p
line solid
draw data 1 1 maxp maxp
    The following output is generated for the BEST CP command. 
                Regression with One Variable
 
---------------------------------------------
 C(p) Statistic            BIC      Variables
---------------------------------------------
      138.73082       59.98154              4
      142.48641       60.30789              2
      202.54876       64.64937              1
      315.15428       70.19729              3
 
 
            Regressions with   2 Variables
 
C(p) =        2.678, BIC =       27.115
---------------------------------------------
       Variable    Coefficient        F Ratio
---------------------------------------------
       X1              1.46831        146.522
       X2              0.66225        208.581
 
 
C(p) =        5.496, BIC =       30.437
---------------------------------------------
       Variable    Coefficient        F Ratio
---------------------------------------------
       X1              1.43995        108.224
       X4             -0.61395        159.294
 
 
C(p) =       22.373, BIC =       41.547
---------------------------------------------
       Variable    Coefficient        F Ratio
---------------------------------------------
       X3             -1.19985         40.295
       X4             -0.72460        100.356
 
 
C(p) =       62.438, BIC =       52.732
---------------------------------------------
       Variable    Coefficient        F Ratio
---------------------------------------------
       X2              0.73133         36.682
       X3             -1.00838         11.816
 
 
C(p) =      138.226, BIC =       62.324
---------------------------------------------
       Variable    Coefficient        F Ratio
---------------------------------------------
       X2              0.31090          0.172
       X4             -0.45694          0.431
 
 
---------------------------------------------
 C(p) Statistic            BIC      Variables
---------------------------------------------
      198.09465       66.81153           1  3
 
 
            Regressions with   3 Variables
 
C(p) =        3.018, BIC =       27.234
---------------------------------------------
       Variable    Coefficient        F Ratio
---------------------------------------------
       X1              1.45194        154.008
       X2              0.41611          5.025
       X4             -0.23654          1.863
 
 
C(p) =        3.041, BIC =       27.271
---------------------------------------------
       Variable    Coefficient        F Ratio
---------------------------------------------
       X1              1.69588         68.715
       X2              0.65691        220.546
       X3              0.25002          1.832
 
 
C(p) =        3.497, BIC =       27.987
---------------------------------------------
       Variable    Coefficient        F Ratio
---------------------------------------------
       X1              1.05184         22.112
       X3             -0.41004          4.235
       X4             -0.64280        208.240
 
 
C(p) =        7.337, BIC =       32.836
---------------------------------------------
       Variable    Coefficient        F Ratio
---------------------------------------------
       X2             -0.92342         12.426
       X3             -1.44797         96.939
       X4             -1.55704         41.654
 
 
            Regressions with   4 Variables
 
C(p) =        5.000, BIC =       29.769
---------------------------------------------
       Variable    Coefficient        F Ratio
---------------------------------------------
       X1              1.55109          4.336
       X2              0.51017          0.497
       X3              0.10191          0.018
       X4             -0.14406          0.041
 
         14 REGRESSIONS          56 OPERATIONS
    The output can be displayed in graphical form. plot generated by sample program

Date created: 08/12/2003
Last updated: 12/11/2023
Please email comments on this WWW page to [email protected].