5. Process Improvement
5.5. Advanced topics
5.5.9. An EDA approach to experimental design

5.5.9.7.

|Effects| plot

Purpose

The |effects| plot answers the question:

What are the important factors (including interactions)?

Quantitatively, the question as to what is the estimated effect of a given factor or interaction and what is its rank relative to other factors and interactions is answered via the least squares estimation criterion (that is, forming effect estimates that minimize the sum of the squared differences between the raw data and the fitted values from such estimates). Based on such an estimation criterion, one could then construct a tabular list of the factors and interactions ordered by the effect magnitude.

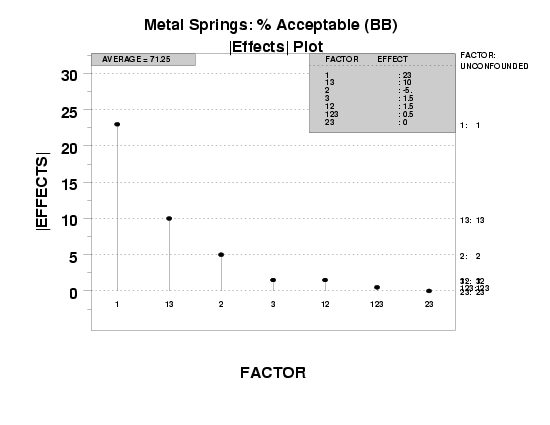
The |effects| plot provides a graphical representation of these ordered estimates, Pareto-style from largest to smallest.

The |effects| plot, as presented here, yields both of the above: the plot itself, and the ranked list table. Further, the plot also presents auxiliary confounding information, which is necessary in forming valid conclusions for fractional factorial designs.

Output

The output of the |effects| plot is:

1. Primary: A ranked list of important effects (and interactions). For full factorial designs, interactions include the full complement of interactions at all orders; for fractional factorial designs, interactions include only some, and occasionally none, of the actual interactions.

2. Secondary: Grouping of factors (and interactions) into two categories: important and unimportant.

Definition

The |effects| plot is formed by:

• Vertical Axis: Ordered (largest to smallest) absolute value of the estimated effects for the main factors and for (available) interactions. For n data points (no replication), typically (n-1) effects will be estimated and the (n-1) |effects| will be plotted.

• Horizontal Axis : Factor/interaction identification:
  1 indicates factor X₁;
  2 indicates factor X₂;
  ...
  12 indicates the 2-factor X₁*X₂ interaction
  123 indicates the 3-factor X₁*X₂*X₃ interaction,
  etc.
  

• Far right margin : Factor/interaction identification (built-in redundancy):
  1 indicates factor X₁;
  2 indicates factor X₂;
  ...
  12 indicates the 2-factor X₁*X₂ interaction
  123 indicates the 3-factor X₁*X₂*X₃ interaction,
  etc.
  If the design is a fractional factorial,the confounding structure is provided for main factors and 2-factor interactions.

• Upper right table: Ranked (largest to smallest by magnitude) list of the least squares estimates for the main effects and for (available) interactions.

  As before, if the design is a fractional factorial, the confounding structure is provided for main factors and 2-factor interactions.

The estimated effects that form the basis for the vertical axis are optimal in the least squares sense. No other estimators exist that will yield a smaller sum of squared deviations between the raw data and the fitted values based on these estimates.

For both the 2^k full factorial designs and 2^k-p fractional factorial designs, the form for the least squares estimate of the factor i effect, the 2-factor interaction effect, and the multi-factor interaction effect has the following simple form:

factor i effect = \( \bar{Y} \)(+) - \( \bar{Y} \)(-)
2-factor interaction effect = \( \bar{Y} \)(+) - \( \bar{Y} \)(-)
multi-factor interaction effect = \( \bar{Y} \)(+) - \( \bar{Y} \)(-)

with \( \bar{Y} \) (+) denoting the average of all response values for which factor i (or the 2-factor or multi-factor interaction) takes on a "+" value, and \( \bar{Y} \)(-) denoting the average of all response values for which factor i (or the 2-factor or multi-factor interaction) takes on a "-" value.

The essence of the above simplification is that the 2-level full and fractional factorial designs are all orthogonal in nature, and so all off-diagonal terms in the least squares X'X matrix vanish.

Motivation

Because of the difference-of-means definition of the least squares estimates, and because of the fact that all factors (and interactions) are standardized by taking on values of -1 and +1 (simplified to - and +), the resulting estimates are all on the same scale. Therefore, comparing and ranking the estimates based on magnitude makes eminently good sense.

Moreover, since the sign of each estimate is completely arbitrary and will reverse depending on how the initial assignments were made (e.g., we could assign "-" to treatment A and "+" to treatment B or just as easily assign "+" to treatment A and "-" to treatment B), forming a ranking based on magnitudes (as opposed to signed effects) is preferred.

Given that, the ultimate and definitive ranking of factor and interaction effects will be made based on the ranked (magnitude) list of such least squares estimates. Such rankings are given graphically, Pareto-style, within the plot; the rankings are given quantitatively by the tableau in the upper right region of the plot. For the case when we have fractional (versus full) factorial designs, the upper right tableau also gives the confounding structure for whatever design was used.

If a factor is important, the "+" average will be considerably different from the "-" average, and so the absolute value of the difference will be large. Conversely, unimportant factors have small differences in the averages, and so the absolute value will be small.

We choose to form a Pareto chart of such |effects|. In the Pareto chart, the largest effects (most important factors) will be presented first (to the left) and then progress down to the smallest effects (least important) factors to the right.

Plot for defective springs data

Applying the |effects| plot to the defective springs data yields the following plot.

How to interpret

From the |effects| plot, we look for the following:

1. The ranked list of factors (including interactions) is given by the left-to-right order of the spikes. These spikes should be of decreasing height as we move from left to right. Note the factor identifier associated with each of these bars.

2. Identify the important factors. Forming the ranked list of factors is important, but is only half of the analysis. The second part of the analysis is to take the ranking and "draw the (horizontal) line" in the list and on the graph so that factors above the line are deemed "important while factors below the line are deemed unimportant.

   Since factor effects are frequently a continuum ranging from the very large through the moderate and down to the very small, the separation of all such factors into two groups (important and unimportant) may seem arbitrary and severe. However, in practice, from both a research funding and a modeling point of view, such a bifurcation is both common and necessary.

   From an engineering research-funding point of view, one must frequently focus on a subset of factors for future research, attention, and money, and thereby necessarily set aside other factors from any further consideration. From a model-building point of view, a final model either has a term in it or it does not--there is no middle ground. Parsimonious models require in-or-out decisions. It goes without saying that as soon as we have identified the important factors, these are the factors that will comprise our (parsimonious) good model, and those that are declared as unimportant will not be in the model.

   Given that, where does such a bifurcation line go?

   There are four ways, each discussed in turn, to draw such a line:

   1. Statistical significance;
   2. Engineering significance;
   3. Numerical significance; and
   4. Pattern significance.

The ranked list and segregation of factors derived from the |effects| plot are to be compared with the ranked list of factors obtained in previous steps. Invariably, there will be a considerable degree of consistency exhibited across all of the techniques.

Conclusions for the defective springs data

The application of the |effects| plot to the defective springs data set results in the following conclusions:

1. Ranked list of factors (including interactions):
   1. X₁ (most important)
   2. X₁*X₃ (next most important)
   3. X₂
   4. other factors are of lesser importance

2. Separation of factors into important/unimportant categories:
   • Important: X₁, X₁*X₃, and X₂
   • Unimportant: the remainder