4. Process Modeling
4.8. Some Useful Functions for Process Modeling
4.8.1. Univariate Functions
4.8.1.2. Rational Functions

4.8.1.2.10.

Cubic / Cubic Rational Function

Function:	${\displaystyle f(x)=\frac{{\beta }_0+{\beta }_{1}x+{\beta }_2{x}^2+{\beta }_3{x}^3}{1+{\beta }_{4}x+{\beta }_5{x}^2+{\beta }_6{x}^3},{\beta }_3\ne 0,{\beta }_6\ne 0}$
Function Family:	Rational
Statistical Type:	Nonlinear
Domain:	${\displaystyle (-\mathrm{\infty },\mathrm{\infty })}$ with undefined points at the roots of ${\displaystyle 1+{\beta }_{4}x+{\beta }_5{x}^2+{\beta }_6{x}^3}$ There will be 1, 2, or 3 roots, depending on the particular values of the parameters. Explicit solutions for the roots of a cubic polynomial are complicated and are not given here. Many mathematical and statistical software programs can determine the roots of a polynomial equation numerically, and it is recommended that you use one of these programs if you need to know where these roots occur.
Range:	${\displaystyle (-\mathrm{\infty },\mathrm{\infty })}$ with the exception that ${\displaystyle y={\beta }_3/{\beta }_6}$ may be excluded.
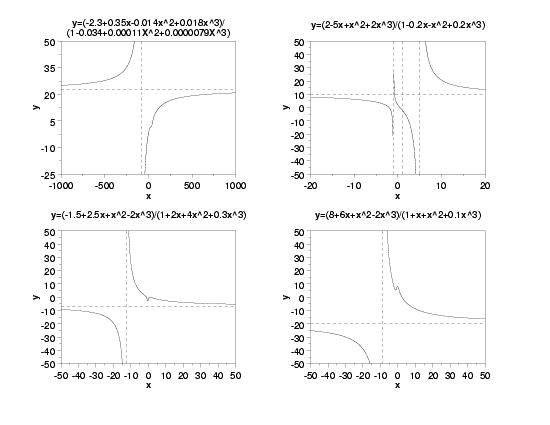
Special Features:	Horizontal asymptote at: ${\displaystyle y={\beta }_3/{\beta }_6}$ and vertical asymptotes at the roots of ${\displaystyle 1+{\beta }_{4}x+{\beta }_5{x}^2+{\beta }_6{x}^3}$ There will be 1, 2, or 3 roots, depending on the particular values of the parameters. Explicit solutions for the roots of a cubic polynomial are complicated and are not given here. Many mathematical and statistical software programs can determine the roots of a polynomial equation numerically, and it is recommended that you use one of these programs if you need to know where these roots occur.
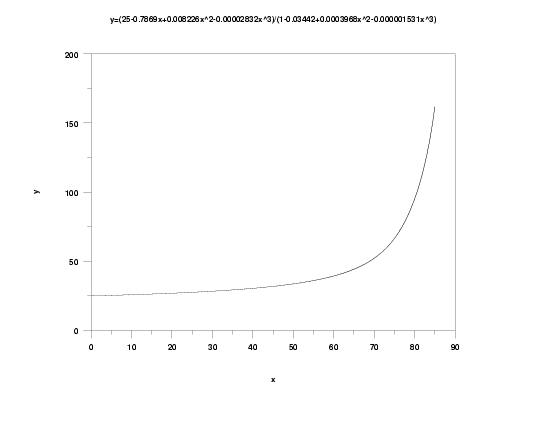
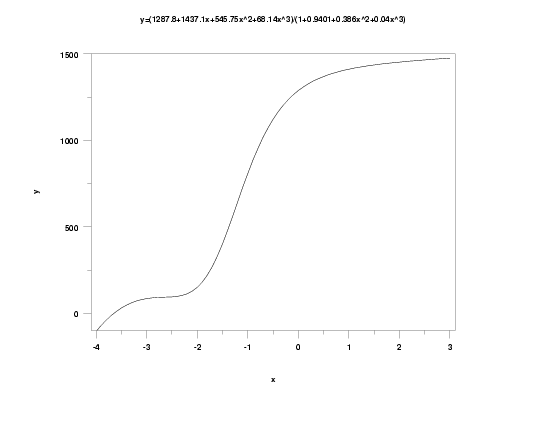
Additional Examples: