4. Process Modeling
4.6. Case Studies in Process Modeling
4.6.4. Thermal Expansion of Copper Case Study

4.6.4.5.

Cubic/Cubic Rational Function Model

C/C Rational Function Model

Since the Q/Q model did not describe the data well, we next fit a cubic/cubic (C/C) rational function model.

Based on the procedure described in 4.6.4.2, we fit the model: $$ y = A_0 + A_1 x + A_2 x^2 + A_3 x^3 - B_1 x - B_2 x^2 - B_3 x^3 + \varepsilon \, , $$ using the following seven representative points to generate the starting values for the C/C rational function.

 TEMP        THERMEXP
 ----        --------
  10             0
  30             2
  40             3
  50             5
 120            12
 200            15
 800            20

The coefficients from the preliminary linear fit of the seven points are:

A0 = -2.323648e+00  
A1 =  3.530298e-01
A2 = -1.383334e-02  
A3 =  1.766845e-04 
B1 = -3.395949e-02 
B2 =  1.100686e-04  
B3 =  7.910518e-06 

Nonlinear Fit Output

The results of fitting the C/C model are shown below.

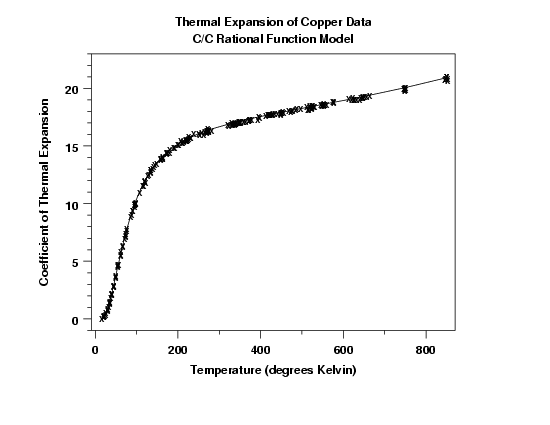
Parameter        Estimate    Stan. Dev    t Value
A0           1.07913        0.1710            6.3
A1          -0.122801       0.1203E-01      -10.2
A2           0.408837E-02   0.2252E-03       18.2
A3          -0.142848E-05   0.2610E-06       -5.5
B1          -0.576111E-02   0.2468E-03      -23.3
B2           0.240629E-03   0.1060E-04       23.0
B3          -0.123254E-06   0.1217E-07      -10.1

Residual standard deviation = 0.0818
Residual degrees of freedom = 229

The regression analysis yields the following estimated model. $$ \hat{y} = \frac{1.079 - 0.122x + 0.004097x^{2} - 0.00000143x^{3}} {1 - 0.00576x + 0.000241x^{2} - 0.000000123x^{3}} $$

Plot of C/C Rational Function Fit

We generate a plot of the fitted rational function model with the raw data.

The fitted function with the raw data appears to show a reasonable fit.

6-Plot for Model Validation

Although the plot of the fitted function with the raw data appears to show a reasonable fit, we need to validate the model assumptions. The 6-plot is an effective tool for this purpose.

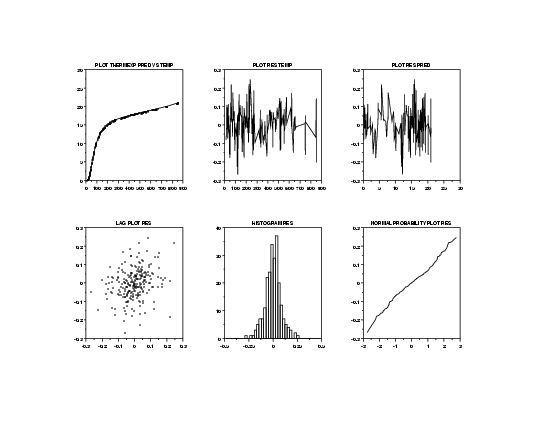
The 6-plot indicates no significant violation of the model assumptions. That is, the errors appear to have constant location and scale (from the residual plot in row 1, column 2), seem to be random (from the lag plot in row 2, column 1), and approximated well by a normal distribution (from the histogram and normal probability plots in row 2, columns 2 and 3).

Residual Plot

We generate a full-sized residual plot in order to show more detail.

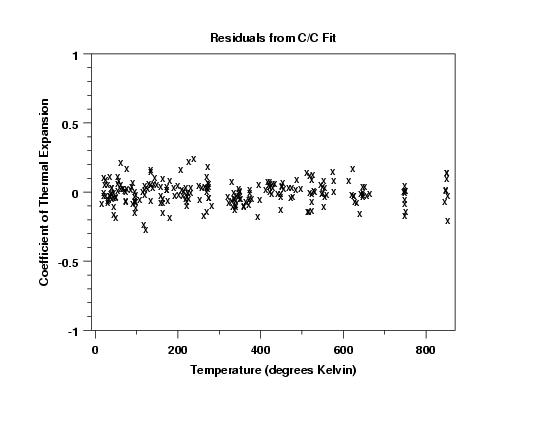
The full-sized residual plot suggests that the assumptions of constant location and scale for the errors are valid. No distinguishing pattern is evident in the residuals.

Conclusion

We conclude that the cubic/cubic rational function model does in fact provide a satisfactory model for this data set.