2.6. Case studies
2.6.5. Uncertainty analysis for extinguishing fire
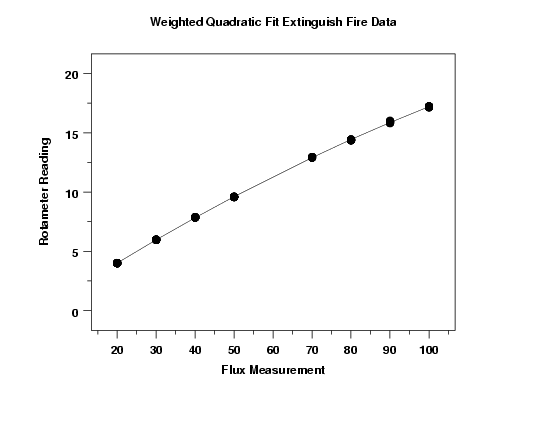
2.6.5.2. Create a calibration curve for the rotameter/a>
2.6.5.2.2. |
Bisquare weighting |
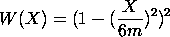
This method provides an effective alternative to deleting specific points. Extreme outliers are deleted, but mild outliers are downweighted rather than deleted altogether. The analysis is shown below.
LEAST SQUARES POLYNOMIAL FIT
SAMPLE SIZE N = 80
DEGREE = 2
REPLICATION CASE
REPLICATION STANDARD DEVIATION = 0.2554919757D-01
REPLICATION DEGREES OF FREEDOM = 72
NUMBER OF DISTINCT SUBSETS = 8
PARAMETER ESTIMATES (APPROX. ST. DEV.) T VALUE
1 A0 -0.147403 (0.1543E-01) -9.6
2 A1 0.217221 (0.6020E-03) 0.36E+03
3 A2 -0.436653E-03 (0.4978E-05) -88.
RESIDUAL STANDARD DEVIATION = 0.0241919290
RESIDUAL DEGREES OF FREEDOM = 77
The fitted weighted quadratic model is
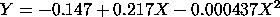
This plot indicates a good fit.
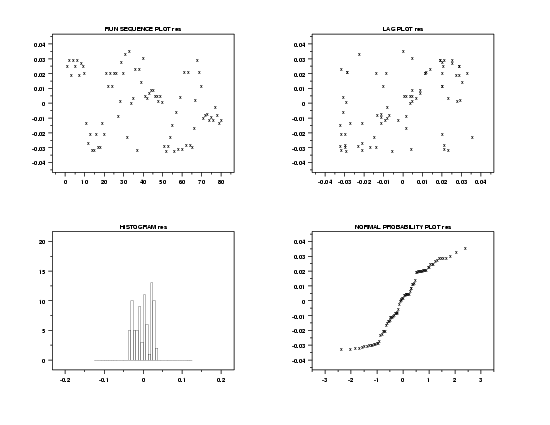
This 4-plot shows that applying the bisquare weighting scheme makes little practical difference in this case.