1.3.3.10.4. Histogram Interpretation: Symmetric and Bimodal

The "mode" of a distribution is that value of the variable which is "most frequent", that is, has the largest probability of occurrence. At the population level, the population mode is the value of the variable corresponding to the peak of the probability density function. At the data level, the sample mode is the value of the data corresponding to the peak of the histogram. The sample mode is, of course, an estimator of the population mode.

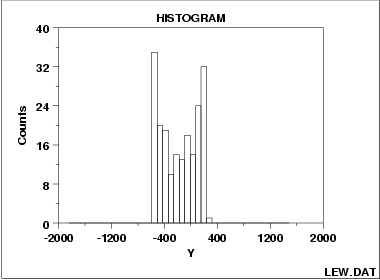
For many phenomena, it is quite common for the distribution of the response values to be unimodel, that is, the data values tend to cluster around a single mode and then distribute themselves with lesser frequency out into the tails. The commonly-encountered bell-shaped normal 9= Gaussian) distribution is the classic example of a unimodal distribution.

The histogram shown above illustrates data from a bimodal (= 2 peak) distribution. If non-unimodality exists, it is important that the analyst be aware of it. As with many of the EDA techniques, the histogram serves as a nice diagnostic tool for increasing such awareness. Questioning as to why such distributional non-unimodality exists frequently leads to greater insight and improved deterministic modeling of the phenomenon under study. (For example, for the data presented above, the bimodal histogram was caused by a deterministic sinusoidality in the data).

Recommended Next Steps

1. Do a run sequence plot or a scatter plot

     to check for sinusoidality.

2. Do a lag plot to check for sinusoidality--

     if elliptical, then sinusoidal.

3. If sinusoidal, then do a spectral plot to

     graphically estimate the

     underlying sinusoidal frequency.

4. If not sinusoidal, then do a Tukey

     lambda PPCC plot to determine

     the best-fit symmetric distribution

     for the data.