Extreme Wind Speeds: Software

• Graph the data
• Determine an appropriate distributional model for the data
• Estimate the parameters of the distribution
• Assess the goodness of fit of the fitted distributional model
• Use the model to estimate quantities of interest

• A run sequence plot of the data is useful for showing time dependent patterns in the data. For extreme value analysis, it can be helpful to draw reference lines at certain threshold values.

• Graphs showing the distributional shape can be useful. The most common types of distributional graphs are histograms and kernel density plots.

• Extreme Value Type I (Gumbel)
• Extreme Value Type II (Frechet)
• Weibull and reverse Weibull
• Generalized Pareto
• Generalized Extreme Value

• The method of moments

• The method of maximum likelihood

• The probability plot correlation coefficient (PPCC)/probability plot method

• For a given distribution, there may be other specialized approaches for estimating the parameters. For the generalized Pareto distribution, the DeHaan and conditional mean exceedance (CME) methods appear to work well in practice.

The PPCC/probability plot method works well for the five extreme value distributions considered here. For the Frechet distribution, using the Kolmogorov-Smirnov plot may improve upon the PPCC plot.

One issue in developing distributional models for extreme winds data is that we typically want a distributional model for the extreme points (i.e., the points above a given threshold) of the data rather than the full data set.

• The Kolgmogorov-Smirnov goodness of fit test can be applied to ungrouped data.

• The Anderson-Darling goodness of fit test is a refinement of the Kolmogorov-Smirnov test. Although the Anderson-Darling test is more powerful than the Kolmogorov-Smirnov test, the critical values must be determined for each different distribution. These critical values have been worked out for the Gumbel, Weibull, and generalized Pareto distributions.

• The chi-square goodness of fit test can be used for grouped data.

• The probability plot provides a graphical assessment of goodness of fit.

  We recommend complementing any quantitative test with a probability plot.

• You can generate a histogram with the fitted distribution overlaid.

• Estimate specific quantiles of the distribution

  Quantiles are estimated from the percent point function (also known as the inverse cumulative distribution function).

• Estimate return intervals and wind speeds corresponding to a given return interval

  The return interval (or mean recurrence interval) of a given wind speed, in years, is defined as the inverse of the probability that the wind speed will be exceeded in any one year. It is defined as

  

  with F(x) denoting the cumulative distribution function.

  More often, we would like to compute the wind speed that corresponds to a given mean return interval. The solution to this is given by solving the above equation for x

  

  with G and R denoting the percent point function and the desired mean recurrence interval, respectively.

  The above formula is for the case of a set consisting of single yearly maxima. If 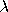is mean number of threshold crossings of the extreme speed record per year, the formula is

  

  See Simiu and Scanlan for a more complete discussion of mean recurrence intervals.

1. Fortran-based Program for Analyzing Hurricane Wind Speeds

2. Fortran-based Program for Analyzing Daily Maximums

3. Dataplot

4. e-FITS web site (currently restricted to NIST staff)

5. Excel-based procedures

6. ASOS data

   Software is provided for extracting wind speed data from ASOS data sets. The software has the capability of extracting separately non-thunderstorm and thunderstorm wind speeds.