|
|
|
Model:
The general statistical model assumed for the nonlinear least squares
regression problems is

where
y denotes the response (dependent) variable,
x denotes predictor (independent) variables and
 (unsubscripted)
denotes the vector of p
unknown parameters to be estimated.
The specific functional form for each dataset is given in the
header information provided on each page.
(unsubscripted)
denotes the vector of p
unknown parameters to be estimated.
The specific functional form for each dataset is given in the
header information provided on each page.
Methodology:
The certified values for the nonlinear least squares regression
problems were obtained using 128-bit precision, with the reported results
confirmed by at least two different algorithms and software packages using
analytic derivatives.
Definitions:
- Estimates of
 , ,
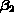 ,... ,...
 , ,
-
The certified values for the estimates,
b =
(b1,
b2,...,
bp)T,
of the true model parameters,
 , ,
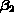 ,... ,...
 ,
are those that produced the smallest residual sum of squares, i.e. ,
are those that produced the smallest residual sum of squares, i.e.

where n denotes the number of observations.
Under the assumption that
 , ,
it follows that these are the maximum likelihood estimators.
- Standard Deviation of the Estimates of
 , ,
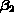 ,... ,...
 , ,
-
The certified values for the standard deviations of the estimates
of the model parameters are the square roots of the diagonal
elements of the asymptotic covariance matrix,

where

J denotes the Jacobian matrix with
ijth element

evaluated at the current values of the parameters,
b1,
b2,...,
bp,
and n and p denote the
number of observations and number of parameters, respectively.
- Residual Sum of Squares
-
The certified value of the residual sum of squares is defined by

where n denotes the number of observations.
- Residual Standard Deviation
-
The certified value of the residual standard deviation is defined by

where n and p denote the
number of observations and number of parameters, respectively.
- Residual Degrees of Freedom
-
The certified value of the residual degrees of freedom is defined by
n-p,
where n and p denote the
number of observations and number of parameters, respectively.
|