|
|
|
Model:
- The general statistical model assumed for the linear least squares
regression problems is

where
y denotes the response (dependent) variable,
 denotes the vector of p
unknown parameters to be estimated and
X
denotes the n
by p matrix of predictor variables.
The specific functional form for each dataset is given in the
header information provided on each page. denotes the vector of p
unknown parameters to be estimated and
X
denotes the n
by p matrix of predictor variables.
The specific functional form for each dataset is given in the
header information provided on each page.
Methodology:
-
For all datasets, multiple precision calculations (accurate to 500 digits) were made
using the preprocessor and FORTRAN subroutine package of Bailey (1995, available from
NETLIB). Data were read
in exactly as multiple precision numbers and all calculations were made with this very
high precision. The results were output in multiple precision, and only then rounded
to fifteen significant digits. These multiple precision results are an
idealization. They represent what would be achieved if calculations were made without
roundoff or other errors. Any typical numerical algorithm (i.e. not implemented in
multiple precision) will introduce computational inaccuracies, and will produce results which differ
slightly from these certified values.
Definitions:
-
- Estimates of

-
The certified values for the estimates,
 ,
of the true parameters, ,
of the true parameters,
 ,
are defined by ,
are defined by
 , ,
the ordinary least squares estimates.
- Residual Sum of Squares and Degrees of Freedom
The certified value for the residual sum of squares is defined by

with the certified value for the residual degrees of freedom defined by n-p.
- Residual Mean Square
The certified value for the residual mean square is defined by

- Residual Standard Deviation
The certified value for the residual standard deviation is defined by

- Standard Deviation of the Estimates of

The certified values for the standard deviations of the estimates of the model parameters are the square roots of the diagonal elements of the variance-covariance matrix

- R-Squared
When the intercept term 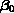 is included in the model, the certified value for R-squared is defined by is included in the model, the certified value for R-squared is defined by

When the intercept term 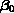 is not included in the model, the certified value for R-squared is defined by is not included in the model, the certified value for R-squared is defined by

- Regression Sum of Squares and Degrees of Freedom
When the intercept term 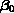 is included in the model, the certified value for the regression sum of squares is defined by is included in the model, the certified value for the regression sum of squares is defined by

with the certified value for the regression degrees of freedom defined by p-1.
When the intercept term 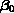 is not included in the model, the certified value for the regression sum of squares is defined by is not included in the model, the certified value for the regression sum of squares is defined by

with the certified value for the regression degrees of freedom defined by p.
- Regression Mean Square
The certified value for the regression mean square is defined by

- F Statistic
The certified value for the F statistic is defined by

|