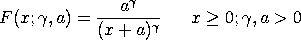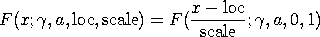PA2CDF
Name:
Type:
Purpose:
Compute the Pareto cumulative distribution of the second
kind with shape parameters
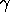 and a.
and a.
Description:
The standard form of the Pareto cumulative distribution
function of the second kind is:
with 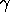 and a denoting the shape parameters. The a
parameter is optional and has a default value of 1.
and a denoting the shape parameters. The a
parameter is optional and has a default value of 1.
The Pareto distribution of the second kind is sometimes
referred to as the Lomax distribution.
Syntax:
LET <y> = PA2CDF(<x>,<gamma>,<a>,<loc>,<scale>)
<SUBSET/EXCEPT/FOR qualification>
where <x> is a variable, a number, or a parameter;
<gamma> is a number or parameter that specifies the
tail length shape parameter;
<a> is a number or parameter that specifies the
optional lower bound shape parameter;
<loc> is a number or parameter that specifies the
optional location parameter;
<scale> is a number or parameter that specifies the
optional scale parameter;
<y> is a variable or a parameter (depending on what
<x> is) where the computed Pareto cdf value is
saved;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.
The a, loc, and scale parameters are all optional.
Examples:
LET A = PA2CDF(3,1.5)
LET X2 = PA2CDF(X1,GAMMA)
LET X2 = PA2CDF(X1,GAMMA,A)
PLOT PA2CDF(X,GAMMA,A) FOR X = 0 0.01 10
Note:
The Pareto cumulative distribution of the second kind can
be extended with location and scale parameters by using the
relationship
Note:
Johnson, Kotz, and Balakrishnan (see Reference section below)
define Pareto distributions of the first, second, third, and
fourth kinds. Dataplot supports Pareto distributions of the
first and second kinds.
Default:
Synonyms:
Related Commands:
|
PA2PDF
|
= Compute the Pareto second kind probability density
function.
|
|
PA2PPF
|
= Compute the Pareto second kind percent point function.
|
|
PARPDF
|
= Compute the Pareto probability density function.
|
|
GEPPDF
|
= Compute the generalized Pareto probability density
function.
|
|
EV1PDF
|
= Compute the extreme value type I probability density
function.
|
|
WEIPDF
|
= Compute the Weibull probability density function.
|
|
NORPDF
|
= Compute the normal probability density function.
|
|
LGNPDF
|
= Compute the lognormal probability density function.
|
|
EXPPDF
|
= Compute the exponential probability density function.
|
Reference:
"Continuous Univariate Distributions: Volume 1", 2nd. Ed.,
Johnson, Kotz, and Balakrishnan, John Wiley, 1994, (chapter 20).
Applications:
Distributional Modeling, Income Distributions
Implementation Date:
Program:
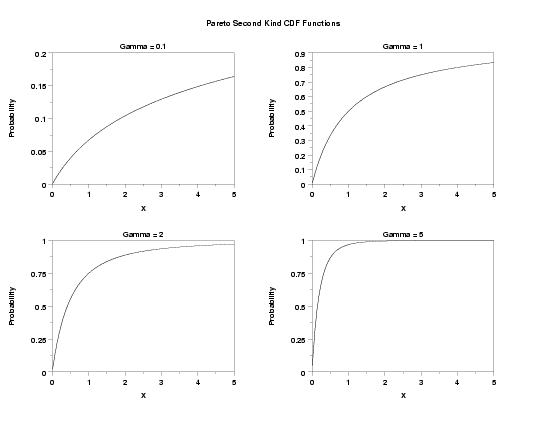
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
.
CASE ASIS
TITLE CASE ASIS
LABEL CASE ASIS
TITLE DISPLACEMENT 2
Y1LABEL DISPLACEMENT 15
X1LABEL DISPLACEMENT 12
Y1LABEL Probability
X1LABEL X
.
LET A = 1
TITLE Gamma = 0.1
PLOT PA2CDF(X,0.1,A) FOR X = 0.01 0.01 5
TITLE Gamma = 1
PLOT PA2CDF(X,1,A) FOR X = 0.01 0.01 5
TITLE Gamma = 2
PLOT PA2CDF(X,2,A) FOR X = 0.01 0.01 5
TITLE Gamma = 5
PLOT PA2CDF(X,5,A) FOR X = 0.01 0.01 5
END OF MULTIPLOT
.
MOVE 50 97
JUSTIFICATION CENTER
TEXT Pareto Second Kind CDF Functions
Date created: 8/23/2006
Last updated: 8/23/2006
Please email comments on this WWW page to
alan.heckert@nist.gov.
|


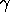 and a.
and a.