GHPDF

GHPDF (LET)

Library Function

Compute the g-and-h probability density function.

The g-and-h distribution is defined in terms of its percent point function:

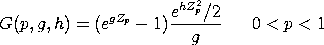
with Z_p denoting the normal percent point function of p. When g = 0 and h = 0, the g-and-h distribution reduces to a standard normal distribution.

The g-and-h probability density function is computed by taking the numerical derivative of the cumulative distribution function (which is turn computed by numerically inverting the percent point function using a bisection method).

The value of g controls the degree of skewness. For g = 0, the distribution is symmetric. As the absolute value of g increases, the amount of the skewness increases. The sign of g controls the direction of the skewness (but not the amount). Positive values of g skew the distribution to the right tail while negative values of g skew the distribution to the left tail. Values for g are typically in the range (-1,1).

The value of h controls the elongation, or how heavy the tails are, of the distribution. For h = 0, the elongation is equivalent to that of a normal distribution. For h = 1, the elongation is equivalent to that of a Cauchy distribution. Values of h are typically in the range (0,1).

Specifying values for both g and h gives this distribution great flexibility in modeling data.

LET <y> = GHPDF(<x>,<g>,<h>,<loc>,<scale>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a variable, number, or parameter;
            <g> is a number or parameter that specifies the skewness shape parameter;
            <h> is a number or parameter that specifies the elongation shape parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed g-and-h pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

Note that the location and scale parameters are optional.

LET A = GHPDF(0.9,0.5,0.2)
LET Y = GHPDF(X,0.5,0.2)
PLOT GHPDF(X,0.5,0.2) FOR X = -5 0.1 5

G-and-h random numbers, probability plots, and goodness of fit tests can be generated with the commands:
LET G = <value>
LET H = <value>
LET Y = GH RANDOM NUMBERS FOR I = 1 1 N
GH PROBABILITY PLOT Y
GH KOLMOGOROV SMIRNOV GOODNESS OF FIT Y
GH CHI-SQUARE GOODNESS OF FIT Y


The following commands can be used to estimate the shape parameters for the g-and-h distribution:

LET G1 = <value>
LET G2 = <value>
LET H1 = <value>
LET H2 = <value>
GH PPCC PLOT Y
GH KS PLOT Y


The default values for G1 and G2 are -1 and 1. The default values of H1 and H2 are H1 and H2.

None

None

GHCDF	= Compute the g-and-h cumulative distribution function.
GHPPF	= Compute the g-and-h percent point function.
LAMPDF	= Compute the Tukey-Lambda probability density function.
NORPDF	= Compute the standard normal probability density function.
LOGPDF	= Compute the logistic probability density function.
JSUPDF	= Compute the Johnson SU probability density function.

"Summarizing Shape Numerically: The g-and-h Distributions", David C. Hoaglin, chapter 11 in "Exploring Data Tables, Trends, and Shapes", Eds. Hoaglin, Mosteller, and Tukey, Wiley, 1985.

Distributional Modeling

2004/5

 
MULTIPLOT 2 2
MULTIPLOT SCALE FACTOR 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
Y1LABEL X
X1LABEL PROBABILITY
X1LABEL DISPLACEMENT 12
Y1LABEL DISPLACEMENT 12
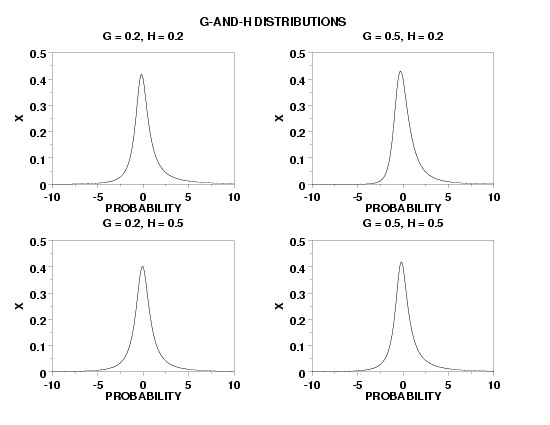
TITLE G = 0.2, H = 0.2
PLOT GHPDF(X,0.5,0.5) FOR X = -10  0.1  10
TITLE G = 0.5, H = 0.2
PLOT GHPDF(X,0.5,0.2) FOR X = -10  0.1  10
TITLE G = 0.2, H = 0.5
PLOT GHPDF(X,0.2,0.5) FOR X = -10  0.1  10
TITLE G = 0.5, H = 0.5
PLOT GHPDF(X,0.5,0.5) FOR X = -10  0.1  10
END OF MULTIPLOT
MOVE 50 97
JUSTIFICATION CENTER
TEXT G-AND-H DISTRIBUTIONS